A regra de três simples é usada para encontrar um quarto valor que não conhecemos, desde que conheçamos apenas três dos valores no problema.
Definição
Chamamos regra de três simples a comparação de duas grandezas proporcionais, relacionando dois valores de uma com dois valores na outra grandeza, sendo que em uma das grandezas um valor é desconhecido.
Como resolver regra de três?
A técnica por trás da resolução de um problema de regra de três simples é separar as grandezas em uma tabela. Este guia mostra os cinco passos necessários para a resolução de um problema.
-
Primeiro separe as grandezas em uma tabela:
- Como se trata de regra de três simples, os valores correspondentes de cada grandeza deve ser colocada em uma coluna da tabela;
-
Identifique se as grandezas são direta ou inversamente
proporcionais:
- As grandezas são inversamente proporcionais quando ao diminuirmos um valor em uma das grandezas, na outra aumenta proporcionalmente, e vice-versa. Já nas grandezas diretamente proporcionais ocorre o contrário das inversamente proporcionais. Quando aumentamos um valor em uma das grandezas, na outra grandeza aumenta proporcionalmente, e vice-versa. Coloque uma seta em sentido contrário para identificar que são inversamente proporcionais;
-
Monte a proporção:
- Pegue os valores de cada grandeza e monte uma proporção, ou seja, igualando as razões;
-
Se for inversamente proporcional, inverta os valores em uma das razões. Esse
passo só deve ser feito caso seja inversamente proporcional:
- Quando as grandezas forem inversamente proporcionais, uma das razões, ou seja, um lado da proporção deve ser invertido;
-
Resolva o problema multiplicando de forma cruzada:
- Multiplique a proporção em forma de X, de forma que o numerador de cada razão da proporção seja multiplicado pelo denominador da outra razão da mesma proporção.
A tabela informada no primeiro passo deve ser montada como a tabela a seguir:
| Grandeza A | Grandeza B |
|---|---|
| a1 | b1 |
| a2 | b2 |
Nessa tabela estamos vendo como separarmos as grandezas, cada grandeza tem dois valores, em uma das grandezas um valor é desconhecido, conhecido como a incógnita do problema.
Como identificar se é inversa ou diretamente proporcional?
Existe dois tipos de regra de três: diretamente proporcional ou inversamente proporcional.
- Diretamente proporcional: as grandezas são diretamente proporcionais quando aumentamos em uma das gradezas, a outra grandeza também aumenta proporcionalmente, e vice-versa;
- Inversamente proporcional: temos gradezas inversamente proporcionais quando aumentamos ou diminuímos uma das grandezas, a outra ocorre o contrário, se uma aumenta a outra diminui, e vice-versa.
Diretamente proporcional
Se as grandezas forem diretamente proporcionais montamos uma proporção em que um dos valores abaixo é desconhecido, assim:
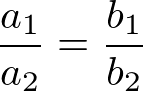
Inversamente proporcional
Se as grandezas forem inversas, então montamos uma das proporções, sendo um dos valores a incógnita, assim:
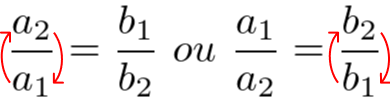
Como é inversamente proporcional invertemos uma das razões, depois calculamos para achar o valor desconhecido.
Exercícios resolvidos
1) Considerando que em uma festa cada 5 pessoas ocupavam uma área de 2 m², qual era a quantidade de pessoas na festa, sabendo que a área do evento era de 800 m²?
Resolução:
Para resolver um problema, podemos seguir o passo a passo descrito acima:
Separar as grandezas em uma tabela.
As grandezas desse problema são: pessoas e área.
| Pessoas | Área |
|---|---|
| 5 | 2 |
| x | 800 |
Montando a tabela logo após separarmos as grandezas, temos que a incógnita está na grandeza pessoas.
Identificar se é direta ou inversamente proporcional. Essa parte é importante para não errar o resultado, vamos analisar.
Se eu aumentar a área de 800 m², a quantidade de pessoas vai aumentar, concorda? Então temos uma regra de três simples diretamente proporcional, ou seja, aumenta em uma razão e também aumenta na outra.
Montamos a proporção.
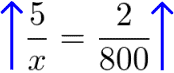
Você, caro leitor, pode usar setas guias para ajudar na resolução do problema. Colocamos uma seta para cima, se aumentarmos a área do evento a quantidade de pessoas também aumenta. Assim, colocamos outra seta para cima no outro lado da proporção indicando que também aumenta.
As setas servem para você lembrar que tem que fazer a inversão se, e somente se, for inversamente proporcional.
Como é direta, precisamos apenas montar a proporção e resolver o problema. Montar uma proporção é colocar as razões em igualdade. Proporção é usada para comparar as grandezas.

Logo, a quantidade de pessoas na festa era de 2000 pessoas.
Multiplicamos de forma cruzada para encontrar o valor de x (a incógnita). Esse valor desconhecido é o que resolve o problema.
2) Se abrirmos 6 torneiras, estas enchem um tanque com água em 22 minutos. Agora, abrindo 4 torneiras apenas, qual é o tempo que leva para o tanque ficar cheio?
Resolução:
Separamos as grandezas agrupando em uma tabela. As grandezas desse problema são:
torneiras e tempo (minutos).
| Torneiras | Tempo |
|---|---|
| 6 | 22 |
| 4 | x |
Montamos a tabela após separarmos as grandezas e agrupar os valores, e vemos que a incógnita está na grandeza tempo.
Identificar se é direta ou inversamente proporcional.
Vamos analisar essa parte crucial do problema. Veja, se eu diminuir a quantidade de torneiras, o tempo para encher o tanque aumenta. Então é inversamente proporcional. Concorda?
Montamos a seguinte proporção.
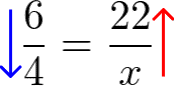
Veja, colocamos a seta azul para baixar para dizer que estamos diminuindo um lado. Agora vamos analisar o comportamento do outro lado. Se diminuirmos de um lado o outro lado aumenta, então colocamos uma seta em sentido contrário.
Essas setas guias servem para você lembrar que tem que fazer a inversão de uma das razões na proporção para não errar no cálculo e encontrar uma resposta diferente. Feito a inversão temos a seguinte proporção:
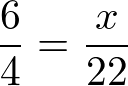
Resolva o problema para encontrar o valor de x.

Logo, para encher o tanque com apenas 4 torneiras precisaremos de 33 minutos.
Veja que multiplicamos a proporção em forma de cruz para encontrar o valor de x. Esse valor desconhecido resolve o problema proposto.
Exercícios propostos
Bons estudos!
Veja também…


