O perímetro do círculo é a medida equivalente à soma do contorno do círculo que é igual ao comprimento da circunferência que limita o círculo.
O círculo é uma figura geométrica limitada pela circunferência. Dessa forma, o perímetro do círculo é igual à medida do contorno da circunferência.

Como o Círculo é Formado?
O círculo é uma figura geométrica formada através de um polígono que ao aumentar a quantidade de lados vai tomando uma forma circular. Como podemos ver na figura:
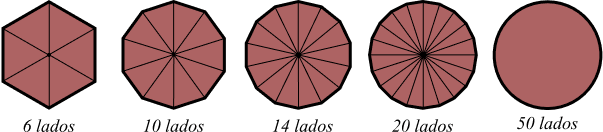
O polígono inicial com 6 lados é um hexágono, aumentando a quantidade de lados ele se torna um decágono (10 lados), com 20 lados o polígono já toma uma forma próxima à forma do círculo. Com 50 lados já não percebemos mais os lados do polígono e já podemos afirmar que o polígono é um círculo.
Analisando a imagem, podemos ver que os polígonos são formados por triângulos unidos ao centro. A área desses polígonos é equivalente a calcular a área de cada triângulo e somar todas as áreas dos triângulos.
Quando o polígono já toma uma forma circular, o cálculo da área é equivalente a usar a fórmula da área do círculo.
Cálculo do Perímetro do Círculo
Para calcular o perímetro do círculo devemos utilizar a fórmula do perímetro da circunferência já que o círculo é limitado pela mesma. Então a fórmula do perímetro é:
P = 2 . π . r
Onde:
- P: é o perímetro;
- π: é o número pi (3,14);
- r: é a medida do raio;
Também podemos calcular o perímetro através da fórmula: P = d.π. Onde d é a medida do diâmetro do círculo.
O diâmetro do círculo também é igual ao diâmetro da circunferência e é igual ao dobro da medida do raio: 2 . r. O raio é a medida do centro até a extremidade da circunferência.
No cálculo do perímetro do círculo a medida que pode variar é a medida do raio, dessa forma o perímetro será maior se a medida do raio for maior. O mesmo vale para o diâmetro.
Área do Círculo
A área do círculo é calculada pela mesma fórmula da área da circunferência, como sabemos que o círculo é limitado pela circunferência. Assim, a fórmula da área do círculo é:
A = π . r²
Onde:
- A: é a área;
- π: é o número pi (3,14);
- r: é a medida do raio;
Leia mais sobre:
Diferença entre Círculo e Circunferência
É comum no estudo de figuras como o círculo e a circunferência houver algumas confusões devido à similaridade dessas figuras. No entanto, existem pequenas diferenças entre essas figuras da Geometria Plana. Veja:
- Círculo: o círculo é a parte interna da figura limitada pelo contorno da circunferência. O círculo é formado por pontos que distam do centro a uma medida menor ou igual à medida do raio.
- Circunferência: a circunferência é o contorno do círculo. É formada por pontos que distam do centro exatamente a medida do raio.

Leia mais sobre:
Exercícios
Acesse os exercícios no link a seguir:


