Múltiplos e Divisores: Aprenda Com Exemplos

Os Múltiplos e Divisores de um número é o conjunto formado por números que são múltiplos ou divisores deste número.

Múltiplos são números que resultam da multiplicação de um número qualquer por qualquer número natural.

Os divisores de um número natural são os números que usamos na multiplicação desse número por outro natural.

Neste artigo vamos estudar em tópicos separados como encontrar os múltiplos e divisores de um número qualquer.

Múltiplos de um número natural

Sejam m e n dois números naturais. Dizemos que n é múltiplo de m, se existir um número k, natural, tal que:

• n = m . k

Exemplo:

Dizemos que 15 é múltiplo de 3, pois existe um número natural k, tal que: 3 . k = 15. Neste caso, k = 5.

Podemos fazer a conta assim:

• 3 . k = 15 ⇔ k = ¹⁵⁄₃ = 5

Para descobrir os múltiplos de um número podemos seguir a seguinte ideia: pegar esse número e multiplicar pelos números naturais.

O conjunto dos múltiplos de um número é infinito.

Conjuntos dos números naturais: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …}

Exemplos:

Múltiplos de 2

Os múltiplos de 2 são quaisquer números que resultam da multiplicação por 2.

• 2 x 0 = 0
• 2 x 1 = 2
• 2 x 2 = 4
• 2 x 3 = 6
• 2 x 4 = 8
• 2 x 5 = 10
• 2 x 6 = 12
• 2 x 7 = 14
• 2 x 8 = 16
• 2 x 9 = 18
• 2 x 10 = 20

Dessa forma, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 e 20 são múltiplos de 2. Os múltiplos de 2 são sempre pares. Perceba que começando com o zero os números foram acrescidos de 2.

Além disso, todos esses números são divisíveis por 2, ou seja, um número que é múltiplo de 2 também é divisível por 2.

Veja alguns múltiplos de 3, 4, 5, 6, 7, 8, 9 e 10:

• Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, …
• Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24, 28, …
• Múltiplos de 5: 0, 5, 10, 15, 20, 25, 30, 35, …
• Múltiplos de 6: 0, 6, 12, 18, 24, 30, 36, …
• Múltiplos de 7: 0, 7, 14, 21, 28, 35, 42, …
• Múltiplos de 8: 0, 8, 16, 24, 32, 40, 48, …
• Múltiplos de 9: 0, 9, 18, 27, 36, 45, 54, …
• Múltiplos de 10: 0, 10, 20, 30, 40, 50, …

12 é múltiplo de 6, pois 6 x 2 é igual a 12. Veja na imagem:

Conseguimos agrupar 12 em dois grupos de 6, isso explica também porque 12 é divisível por 6, porque conseguimos dividir 12 em 2 grupos de 6.

A tabuada de multiplicação é formada pelos múltiplos de um número.

Divisores de um número natural

Sejam m e n dois números naturais. Dizemos que m é divisor de n, se existir um número k, natural, tal que:

• m . k = n

Exemplo:

Dizemos que 3 é divisor de 15, pois existe um número natural k, tal que: 3 . k = 15. Neste caso, k = 5.

Podemos, também, fazer a conta assim:

• 3 . k = 15 ⇔ k = ¹⁵⁄₃ = 5

Portanto, podemos dizer que os divisores de um número são quaisquer números que divididos por ele tem resto zero, divisão exata.

Exemplo:

Dizemos que 10 é divisível por 2 ou 2 é divisor de 10, pois 10 dividido por 2 é 5, uma divisão exata.

Se 12 é divisível por 3, assim 3 é divisor de 12, portanto 12 é múltiplo de 3.

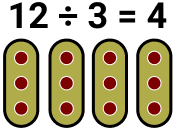
Veja na imagem que ao dividirmos 12 por 3 temos uma divisão exata, ou seja, não sobra nada. Conseguimos dividir 12 em 4 partes iguais.

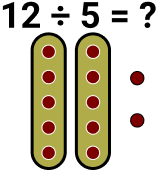
Agora veja que 12 não é divisível por 5, pois não temos uma divisão exata, ou seja, sobra dois, tem resto 2. Não conseguimos dividir 12 em partes iguais.

O conjunto dos divisores de um número é sempre finito e menor que este número.

Exemplo:

• Conjuntos dos divisores de 12: 1, 2, 3, 4, 6 e 12.
• Conjuntos dos divisores de 50: 1, 2, 5, 10, 25 e 50.

Números primos e sua relação com os múltiplos e divisores

Os números primos são números que possuem apenas dois divisores, o número 1 e ele mesmo.

Exemplo:

• Divisores de 5: 1 e 5.
• Divisores de 13: 1 e 13.
• Divisores de 31: 1 e 31.

Por outro lado, com um número primo podemos encontrar diversos divisores, que são os números que multiplicamos por ele.

Exemplo:

• Múltiplos de 5: 5, 10, 15, 20, 25, …

Para encontrar os múltiplos de um número primo devemos realizar o mesmo processo para encontrar os múltiplos de um número natural qualquer. Sem segredo!

Entender quais são os múltiplos e divisores de um número é bem simples. Assim, quando ouvi falar sobre o assunto, você já deve saber do que se trata.

Exercícios

Veja os exercícios propostos no link abaixo:

• Exercícios sobre múltiplos e divisores

Bons estudos.