Juros simples é uma remuneração dada a alguém pela aplicação de seu capital em um determinando período. Esse regime de juros é calculado aplicando uma taxa em relação ao capital aplicado inicialmente.
É muito utilizado do dia a dia quando emprestamos dinheiro a outra pessoa, por exemplo.
Ao emprestarmos queremos receber uma quantia a mais pelo empréstimo e isso nada mais é do que uma vantagem que queremos pelo empréstimo. Uma espécie de: te empresto, mas quero que me pague a mais por isso.
A pessoa que empresta a outra certa quantia, recebe uma remuneração a mais além do valor emprestado, e isso é o que denomina juros.
Devemos aplicá-lo a uma transação considerando essas quatro variáveis:
- Capital: é o valor aplicado;
- Juros: é o acréscimo que recebe pelo valor aplicado;
- Tempo: o tempo dado para receber o valor aplicado de volta mais os juros;
- Taxa: taxa aplicada, em porcentagem, que determina a quantidade de juros incidente sobre o capital inicial.
Para efeito de cálculo, os juros são diretamente proporcionais ao capital, ao tempo e a taxa.
Veja estes exercícios propostos.
Fórmula
Vamos estabelecer que o capital será representado pela letra C, maiúscula, o tempo pela letra t, minúscula, a taxa por i, também minúscula, e os juros pela letra J, maiúscula. Assim, temos a seguinte fórmula:
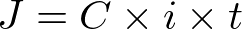
Quando aplicamos esta fórmula, devemos ficar atentos aos seguintes casos:
- Se a taxa for ao ano, o tempo deve ser reduzido à unidade de ano;
- Caso seja ao mês, o tempo deve ser reduzido à unidade de mês;
- Se a taxa for ao dia, o tempo deve ser reduzido à unidade de dia.
Observações:
- A taxa i deve ser colocada na forma decimal.
- Exemplo: se a taxa for 5%, então i = 0,05, que é a divisão de 5 por 100.
- A taxa e o tempo devém está nas mesmas unidades.
- Exemplo: se a taxa for 3% ao mês, o tempo também deve ser representado em meses. Dessa forma, se o tempo estiver em ano, converta-o em meses.
Montante
Chamamos montante, representado pela letra maiúscula M, a soma do capital inicial mais os juros obtidos na aplicação. Ou seja, quando uma pessoa que aplica um valor, e depois faz o resgate desse valor aplicado mais os juros recebidos, esse é o montante.
Fórmula para o cálculo do Montante
Para determinarmos o montante, utilizamos a seguinte fórmula:

Onde:
- M é o montante;
- C é o capital aplicado;
- J são os juros aplicados, definido pela primeira fórmula acima.
Observe que os juros são calculados pela fórmula abaixo:
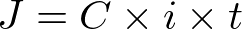
Então, substituindo a fórmula acima na fórmula do montante M, temos:

Portanto, temos que o montante também pode ser calculado pela fórmula:
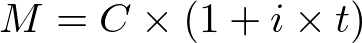
Responda estes exercícios propostos.
Juros Compostos
Além dos juros estudados nesse artigo, temos também outra forma de calcular juros que são os juros compostos.
Este tipo de correção financeira é usada com frequência nas instituições financeiras, pois oferecem uma melhor rentabilidade.
Os juros compostos são aplicados no capital inicial mais os juros dos meses anteriores, isto é, a partir do segundo mês a rentabilidade é calculada sobre o capital inicial mais os juros dos meses anteriores.
Exercícios resolvidos
(FEC) Um jovem que trabalha com artes gráficas decidiu comprar um computador para poder desenvolver melhor suas atividades. Ao decidir pela configuração que precisava constatou que seriam necessários R$2.490,00 para adquirir o seu computador à vista. Como isso estava totalmente fora do seu orçamento resolveu negociar a compra do equipamento a prazo, o que só foi possível mediante acréscimo de juros de 30% ao ano, aplicado ao valor à vista por oito meses. O pagamento foi feito em oito prestações mensais iguais, cada uma no valor de:
- A) R$ 373,50
- B) R$ 498,00
- C) R$ 2.988,00
- D) R$ 1.992,00
Resolução:
Calculando o valor do acréscimo:
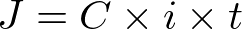
onde:
- J: o valor dos juros a ser determinado
- C: R$2.490,00 (valor do capital aplicado)
- i: 30% a.a. (taxa percentual anual)
- t: 8 meses (período de aplicação)
Nas fórmulas de matemática financeira, tanto o prazo da operação (t) como a taxa (i) devem, necessariamente, está expresso na mesma unidade de tempo.
Assim, transformando a taxa percentual anual, em taxa percentual mensal, temos:
- (30% a.a.) ÷ 12 = 2,5% a.m.
Então, temos que:

O Montante a ser pago no final do período da aplicação, ou seja, o capital empregado mais a rentabilidade adquirida será de:
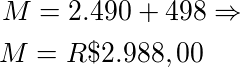
De acordo com o enunciado, o pagamento foi feito em oito prestações mensais iguais, então, cada prestação terá um valor de:
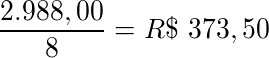
Resposta: A
(UFMG) Um consumidor adquiriu determinado produto em um plano de pagamento de 12 parcelas mensais iguais de R$ 462,00, a uma taxa de 5% ao mês. Ele pagou as 10 primeiras prestações no dia exato do vencimento de cada uma delas. Na data do vencimento da 11.ª prestação, o consumidor decidiu quitar a última também, para liquidar sua dívida. Ele exigiu, então, que a última prestação fosse recalculada, para a retirada dos juros correspondentes ao mês antecipado, no que foi atendido. Após recalculado, o valor da última prestação passou a ser de
- A) R$ 438,90
- B) R$ 441,10
- C) R$ 440,00
- D) R$ 444,00
Resolução:
Analisando a questão, temos que o consumidor exige que a última parcela seja recalculada, retirando os juros.
Sendo assim, temos que descontar da última parcela de R$ 462,00, paga 1 mês antes, 5% de juros.
Logo, devemos realizar o seguinte cálculo para corrigir a taxa: 100% + 5% = 105/100 = 1,05
A taxa de juros em cada parcela foi de um aumento de 5%. Assim, considere P a parcela sem a aplicação dos juros, então:
- 1,05 . P = 462 ⇒ P = 462 / 1,05 = 440
Logo, a última parcela será de R$ 440,00, alternativa C.
Exercícios propostos
Acesse os exercícios no link abaixo:
Leia também…



