A função linear é uma função f: R → R definida como f(x) = ax. É uma função especial da função do primeiro grau f(x) = ax + b. Isto é, é um caso especial da função do 1º grau, quando b = 0.
Definição
Seja uma função f: R → R, a função linear é definida como f(x) = ax, com a ∈ R e a ≠ 0.
O valor a que acompanha a variável x na função é chamado de coeficiente angular. É o coeficiente que determina a direção do gráfico da função. Se for negativo, o gráfico da função é decrescente, caso contrário, será crescente.
Além disso, quando o valor do coeficiente for igual a 1, a chamamos de função identidade.
Gráfico
O gráfico no plano cartesiano é um gráfico que sempre passa pela origem do plano, ou seja, pelo ponto (0, 0).
A inclinação da reta que determina o gráfico é dado pelo valor do coeficiente a.
Exemplos de gráficos:
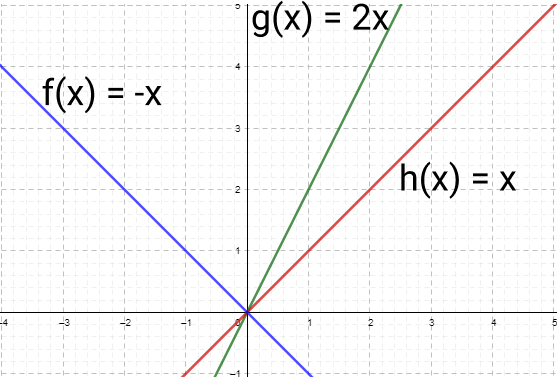
Para g(x) o coeficiente a tem valor 2, para f(x), a = -1 e para h(x), a = 1.
Função Linear Crescente e Decrescente
A função é classificada em crescente e decrescente. O que determina o tipo é o valor do coeficiente angular. Dessa forma, uma função linear é crescente quando o valor do coeficiente é positivo, e decrescente quando negativo.
Exemplo:
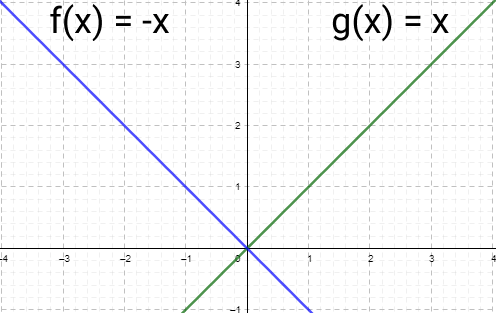
O coeficiente angulara em g(x) é 1 e em h(x) é -1
Exercícios
Veja os exercícios que preparamos no link a seguir:

