Fração é a forma de dividir algo através da razão de dois números inteiros. Dessa forma, nada mais é do que uma divisão onde o dividendo é numerador e o divisor é o denominador.
Quando dividimos uma pizza, por exemplo, estamos fracionando-a. Cada fatia representa uma parte da pizza, ou seja, uma fração. Geralmente ela é dividida em 8 pedaços, então cada pedaço representa 1⁄8 (um oitavo) de uma pizza.
Como representar uma fração?
Podemos representar uma fração através da escrita em números ou de forma visual, através de desenhos para melhor o entendimento. Vamos mostrar às duas formas.
Representação escrita de frações
Uma fração é representada, de forma escrita, por dois números inteiros, sendo um, o numerador, e o outro, o denominador.
Exemplo:
Considere
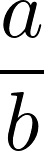
Onde a é o numerador, o número que fica acima, e b, o denominador, o número que fica embaixo.
Representação gráfica de frações
As frações também são representadas de forma gráfica. O aluno pode encontrar outra forma de representação gráfica, como, por exemplo, retângulos.
Nós vamos mostrar a forma usual de representação gráfica, os gráficos de pizza.
Vejas alguns exemplos:





Imagine uma pizza dividida em oito pedaços iguais, e caso exista quatro pessoas para comê-la. Se todos comerem dois pedaços, assim cada pessoa comeu 2⁄8 (dois oitavos) de pizza.
Agora imagine que oito pessoas comeram um pedaço cada uma, dessa forma, cada pessoa comeu 1⁄8 (um oitavo) de pizza.
Tipos de frações
Frações equivalentes
Frações equivalentes são frações que representam a mesma quantidade. Se quisermos encontrar frações que são equivalentes para uma fração, basta multiplicarmos o numerador e denominador pelo mesmo número natural diferente de zero.
Exemplo:
Encontrar frações equivalentes para 1⁄3. Vamos multiplicar 1⁄3 por 2, 3, 4 e 5.
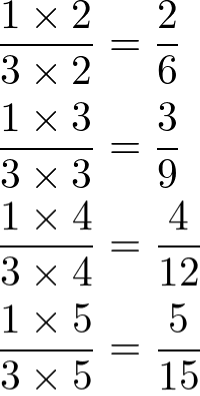
Assim, 2⁄6, 3⁄9, 4⁄12, 5⁄15 são frações equivalentes para 1⁄3.
Para verificar se duas frações são equivalentes, basta multiplicar em forma cruzada.
Vamos verificar se 1⁄3 é realmente equivalente a 5⁄15.

Obtemos uma igualdade, portanto 1⁄3 e 5⁄15 são realmente equivalentes.
Frações Próprias
São frações quando o numerador é menor que o denominador.
Exemplo: 1⁄2, 3⁄8, 5⁄8, etc.
Frações Impróprias
São frações quando o numerador é maior ou igual ao denominador.
Exemplo: 5⁄3, 7⁄2, 2⁄2, etc.
Frações Aparentes
São frações onde o numerador é múltiplo do denominador.
Exemplo: 9⁄3, 6⁄2, 20⁄5, etc.
Veja que se multiplicarmos o denominador por um número natural encontramos o numerador, por exemplo: 9⁄3, o numerador é o denominador multiplicado por 3.
Frações aparentes são números inteiros representados em fração, isto é, 3 também pode ser representado por 9⁄3 ou 6⁄2.
Frações Mistas
São frações aonde parte dela é um número inteiro e a outra parte é uma fração.
Exemplo:
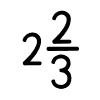
é equivalente a 8⁄3.
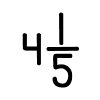
É equivalente a 21⁄5, veja a seguir no próximo tópico essa equivalência.
Conversão de Frações Mistas e Impróprias
Conversão de fração imprópria em fração mista
Para transformar uma fração imprópria em uma mista, basta dividir a fração pelo denominador, sendo que a parte inteira será o quociente, o resto será o numerador e o divisor será o denominador.
Exemplo:
Considere a fração imprópria 21⁄5.
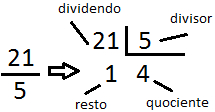
Dessa forma, o quociente 4 vira a parte inteira, o resto 1, o numerador, e o divisor 5 será o denominador. Assim, temos a fração mista.
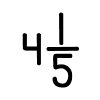
equivalente a 21⁄5.
Conversão de fração mista em fração imprópria
Para fazer o processo inverso, isto é, transformar a fração mista em uma imprópria, basta conservar o denominador, depois multiplicá-lo pela parte inteira e somar com o numerador.
Exemplo:
Considere a fração mista do exemplo anterior
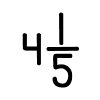
Vamos transformá-la de volta para 21⁄5. Dessa forma, conservamos o denominador 5, multiplicamos o denominador 5 por 4 e somamos com o numerador 1. Veja:
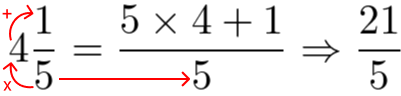
Frações Compostas ou Complexas
Frações compostas ou complexas são frações onde o numerador e o denominador também são frações.
Exemplo:
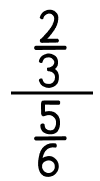
Frações Unitárias
São frações onde o numerador é o número 1 e o denominador pode ser qualquer valor inteiro maior que zero.
Exemplo: 1⁄5, 1⁄100, etc.
Frações Decimais
São frações onde o denominador é uma potência positiva de 10 e estas podem ser representadas também na forma decimal.
Exemplos:
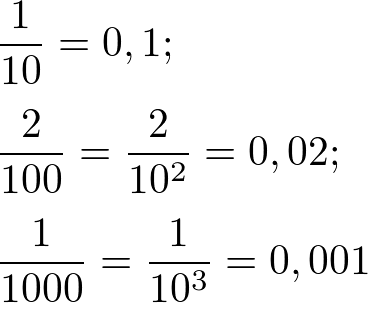
Frações Ordinárias
Frações ordinárias são frações da forma
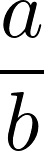
Sendo a um inteiro qualquer e b um inteiro positivo maior que zero.
Exemplo: –10⁄3, 2⁄5, etc.
Simplificação de Frações e Frações Irredutíveis
Simplificação de frações é uma redução da fração original em outra fração equivalente com números menores.
Para simplificar uma fração temos que dividir o numerador e o denominador da fração pelo máximo divisor comum aos números em questão.
Quando temos uma fração com valores altos no numerador e denominador podemos simplificá-la encontrando uma fração equivalente com valores menores e irredutível.
A simplificação ajuda na resolução de problemas complexos, de forma que encontremos a solução mais rapidamente. Vamos entender com um exemplo:
Exemplo:
Considere a fração 20⁄100. Podemos simplificá-la dividindo o numerador e denominador pelo mesmo valor, esse valor é o máximo divisor comum, entenda como encontrar aqui, o MDC de 20 e 100 é 20:
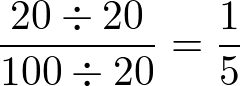
Dessa forma, 1⁄5 é uma fração equivalente e simplificada de 20⁄100, também chamada fração irredutível, isto é, não é mais possível reduzi-la, simplificá-la.
Também pode ser simplificada dividindo o numerador e denominador pelo menor número que divide ambos. Dessa forma não é preciso calcular o MDC. Porém, neste caso, temos mais trabalho.
Exemplo:
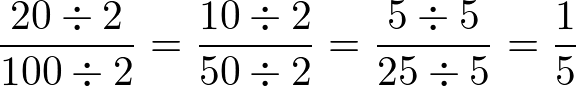
O que fizemos foi dividir o numerador e denominador da fração pelo menor número que divide ambos, neste caso 2. Depois continuamos dividimos por 2, pois ainda era possível continuar dividindo por esse valor.
Por fim, obtemos 5⁄25 que somente podiam ser divididos por 5. Encontramos a fração irredutível 1⁄5 que não pode mais ser simplificada.
Portanto, podemos dizer que 20⁄100 é equivalente a 1⁄5 ou que 1⁄5 é a fração simplificada ou irredutível de 20⁄100.
Comparação de frações
Comparação de frações é uma forma de analisar qual delas representam a maior quantidade ou a maior parte de um todo. Existem duas formas de comparar frações, veja:
Denominadores iguais
Se os denominadores forem iguais basta analisar o numerador.
Exemplo:
Considerem-se as frações: 3⁄5 e 1⁄5
Os denominadores são iguais, então vamos analisar somente os numeradores. Então, como 3 é maior que 1, assim:
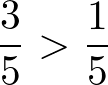
Podemos entender assim: considere um bolo dividido em 5 pedaços. Se eu comer 3 pedaços e meu irmão comer 1 pedaço, então eu comi mais que ele. Logo: 3⁄5 maior que 1⁄5.
Denominadores diferentes
Se os denominadores forem diferentes temos que utilizar uma regra básica que faz com que as frações fiquem com denominadores iguais e possamos utilizar o primeiro caso.
Exemplo:
Considerem-se as frações: 5⁄2 e 7⁄3
Estas frações têm denominadores diferentes e não podemos utilizar o primeiro caso. Para transformá-las em frações com denominadores iguais, pegamos o denominador de uma fração e multiplicamos na outra. Veja:
5⁄2 tem denominador 2, vamos multiplicar 7⁄3 por 2; 7⁄3 tem denominador 3, vamos multiplicar 5⁄2 por 3;
Portanto,
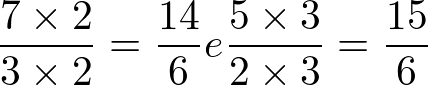
Dessa forma, temos duas frações com denominadores iguais e podemos utilizar o primeiro caso. Então, temos que
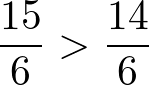
Portanto,
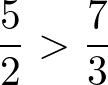
Simples, não é?
Exercícios
Responda os exercícios de frações para fixar o aprendizado


