Os exercícios a seguir foram preparados para você praticar e, assim, memorizar o conteúdo estudado sobre coeficiente angular.
1) Calcule o coeficiente angular da reta que passa pelos pontos A(2, 3) e B(-3, 4).
Ver resposta
Calculamos o coeficiente angular m utilizando a fórmula:
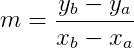
Então: m = (4 – 3)/(-3 – 2) = – (1/5)
2) Encontre a equação de uma reta com coeficiente angular m = 3/2, sabendo que ela passa pelo ponto A(5, 7).
Ver resposta
Respondemos esta questão substituindo na equação os dados do problema:
Assim:
y – y0 = m(x – x0) ⇒
y – 7 = (3/2)(x – 5) ⇒
y – 7 = (3/2)x – 15/2 ⇒
y – 7 – (3/2)x + 15/2 = 0 ⇒
– (3/2)x + y + 1/2 = 0
3) Determine a equação da reta que passa pelo ponto A(3, 5) e que possui uma inclinação de 45°.
Ver resposta
O coeficiente angular é dado pela tangente do angulo de 45°, a tangente de 45° é 1.
Então, substituindo temos:
y – y0 = m(x – x0) ⇒
y – 5 = 1(x – 3) ⇒
y – 5 = x – 3 ⇒
y – 5 – x + 3 = 0 ⇒
-x + y – 2 = 0
4) Desenhe no plano cartesiano a reta que passa pelos pontos A(-2, 3) e B(3, 1) e calcule o seu coeficiente angular.
Ver resposta
Plano cartesiano:
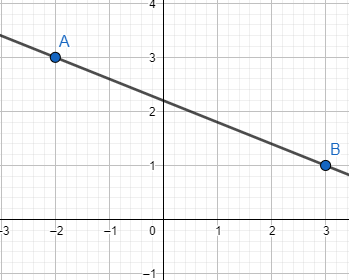
imagem do geogebra
Coeficiente angular:
m = (1 – 3)/(3 – (-2)) = – 2/5
5) Escreva a equação da reta da questão 4 na forma y = mx + b e determine o coeficiente linear b.
Ver resposta
Já sabemos o coeficiente angular da reta, m = – 2/5. Então, substituindo em y = mx + b, temos: y = -2/5x + b
Pela questão, temos que a reta passa pelo ponto A(-2, 3), então, substituindo, temos: y = -2/5x + b ⇒ 3 = -2/5(-2) + b ⇒ 3 = 4/5 + b ⇒ b = 3 – 4/5 ⇒ b = 11/5
Portanto, temos que a equação da reta é: y = -2/5x + 11/5
6) Determine a equação da reta que passa pelo ponto A(-6, 2) e é paralela a x + 3y = 4.
Ver resposta
Veja que podemos reescrever a equação da reta x + 3y = 4 como y = -x/3 + 4/3. Uma reta paralela a outra possui o mesmo coeficiente angular.
Portanto, a equação da reta que passa pelo ponto A(-6, 2) é:
y = mx + b ⇒
2 = -(-6/3)) + b ⇒
2 = 2 + b ⇒
b = 0
Assim, a equação da reta que passa pelo ponto e é paralela é: y = -x/3 + 0
Estes exercícios são suficientes para entender como calcular o coeficiente angular.

