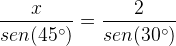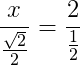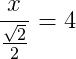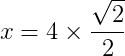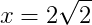Responda os exercícios abaixo sobre trigonometria para treinar os seus conhecimentos.
1) Determine a medida x e y do triângulo retângulo a seguir. (Considere: sen(62,1°) = 0,88; cos(62,1°) = 0,47)
Ver resposta
Cálculo da medida de x:
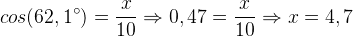
Cálculo da medida de y:
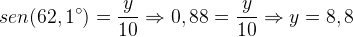
2) Determine sen(2x), sabendo que tg(x) + cotg(x) = 8.
Ver resposta
Pela questão temos que:
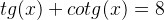
Usando a relação fundamental para a tg(x) e cotg(x), temos:
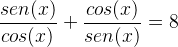
Assim,
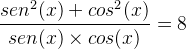
sen²(x) + cos²(x) = 1
Logo,
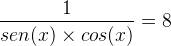
Podemos escrever assim:
sen(x) . cos(x) = 1/8
Como,
sen(2x) = 2 . sen(x) . cos(x)
Então,
sen(2x) = 2 . 1/8 = 2/8 = 1/4
3) Esboce o gráfico para a função f(x) = 3 + sex(x). Determine também a imagem e o domínio da função.
Ver resposta
O gráfico de f(x) tem o seguinte aspecto:
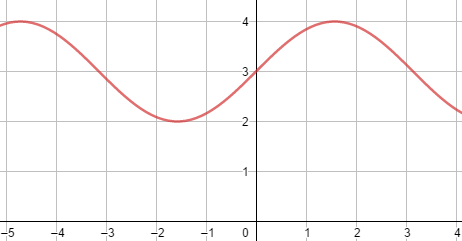
A imagem da função f(x) = 3 + sen(x) é obtida atribuindo os valores máximo e mínimo de sen(x).
Então, aplicando os valores extremos de f(x), temos:
f(-1) = 3 + (-1) = 2
f(1) = 3 + 1 = 4
Portanto, a imagem de f é: Im = [2, 4].
O domínio da função f(x) = 3 + sex(x) é definido para todos os valores reais, portanto, D = R
4) Determine o período, esboce o gráfico e determine as imagens para as funções a seguir:
a) f(x) = 2 sen(x)
b) f(x) = cos(7x)
c) f(x) = – cos(x)
d) f(x) = 1 – cos(4x)
e) f(x) = 1 + sen(-x)
Ver resposta
a) f(x) = 2 sex(x)
Período da função seno ou cosseno é dado pela fórmula:
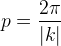
Onde k é o termo que acompanha o x.
Então o período da função acima é: p = 2π/1 = 2π
Gráfico:
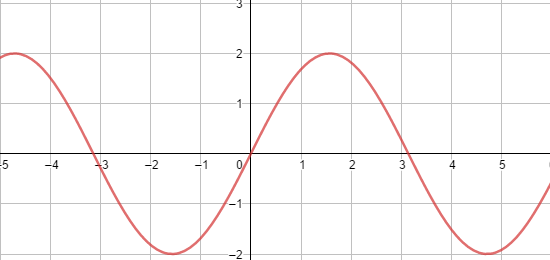
A imagem de f(x) = 2 sen(x) é encontrada aplicando os valores máximos e mínimos da função sen(x), que é -1 e 1. Então:
f(-1) = 2 . (-1) = -2
f(1) = 2 . 1 = 2
O conjunto imagem é: Im f(x) = [-2, 2]
b) f(x) = cos(7x)
Período da função, aplicando a fórmula:
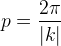
p = 2π/7, pois k = 7, termo que acompanha o x.
Gráfico:
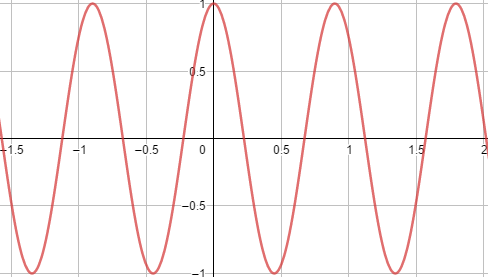
Imagem:
f(-1) = -1
f(1) = 1
Logo, Im f(x) = [-1, 1]
c) f(x) = – cos(x)
Período:
p = 2π/k = 2π/1 = 2π
Gráfico:
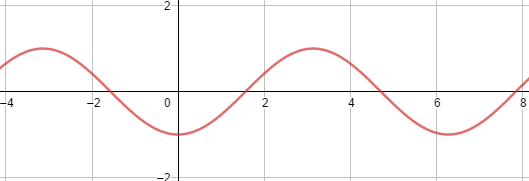
Imagem: f(x) = – cos(x)
Aplicando os valores extremos da função cosseno (-1, 1), temos:
f(-1) = -(-1) = 1
f(1) = – 1
Portanto, Im f(x) = [-1, 1]
d) f(x) = 1 – cos(4x)
Período:
p = 2π/k = 2π/4 = π/2
Gráfico da função:
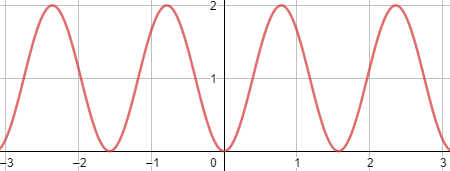
Imagem de f:
f(-1) = 1 – (-1) = 2
f(1) = 1 – 1 = 0
Portanto, a imagem de f(x) = 1 – cos(4x) é: [0, 2]
e) f(x) = 1 + sen(-x)
Período da função f(x) = 1 + sen(-x).
Usando a fórmula: p = 2π/k = 2π/(-1) = -2π
Gráfico da função:
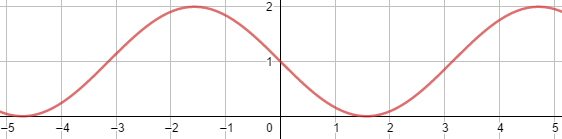
Imagem de f(x) = 1 + sen(-x):
f(-1) = 1 – 1 = 0
f(1) = 1 + 1 = 2
Portanto, Im f(x) = [0, 2]
5) (FATEC) Se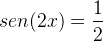 
, então 
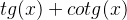é igual a:
a) 8
b) 6
c) 4
d) 2
e) 1
Ver resposta
Temos que:
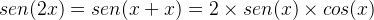
Então
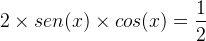
Logo,
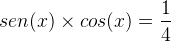
Então podemos usar a relação trigonométrica derivada das funções básicas da trigonométrica para a tg(x) e cotg(x).
Portanto, temos:
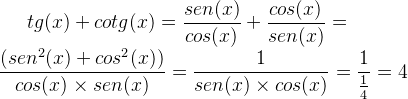
Resposta C.
6) Quanto mede um arco de
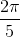
radianos em graus?
Ver resposta
Sabemos que π = 180° e alguns ângulos em radiano ficam em função de π. Vamos trocar π por 180°. Assim:
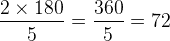
Portanto, 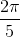radianos igual a 72°.
Dica: se a medida for em número real, utilize regra de três simples.
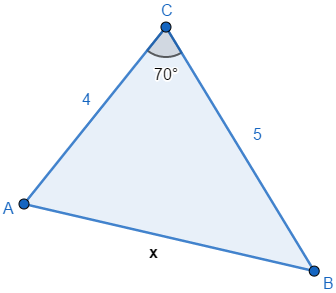
7) Determine o valor de x no triângulo abaixo (Use: cos(70°) = 0,34; sen(70°) = 0,94):
Ver resposta
Pela lei dos cossenos temos que:
x² = b² + c² – 2 . b . c . cos(70) ⇒ x² = 5² + 4² – 2 . 5 . 4 . 0,34 ⇒ x² = 25 + 16 – 13,6 ⇒ x² = 41 – 13,6 ⇒ x = √27,4 = 5,23
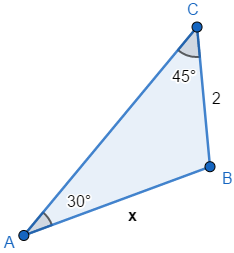
8) Determine a medida de x no triângulo abaixo:
