Aprenda a simplificar frações com raízes no denominador. Esse processo é chamado racionalização de denominadores e podemos praticar com os exercícios a seguir:
1) Racionalize o denominador da fração:

Ver resposta
A racionalização de denominadores em frações com raízes no denominador consiste em eliminar a raiz do denominador.
Para fazer isso, multiplicamos a raiz pelo denominador e pelo numerador. Veja:
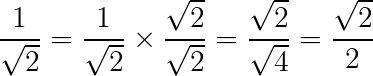
Dessa forma, eliminamos a raiz.
2) Racionalize a fração:

Ver resposta
Precisamos eliminar √3 do denominador da fração, então multiplicamos o numerador e denominador por √3. Veja:
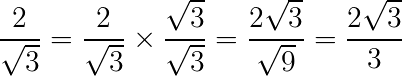
3) Racionalize a fração:

Ver resposta
Vamos eliminar 2√2 do denominador da fração, assim temos:
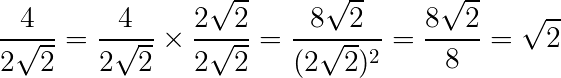
4) Racionalize a fração:

Ver resposta
Nesta questão, não temos somente uma raiz no denominador, temos a soma de uma raiz por um número inteiro. Aqui para eliminar a raiz temos que multiplicar o numerador e denominador pelo conjugado de √2 + 1 que é √2 – 1, ou seja, o conjugado de √2 + 1 é só trocar o sinal. Assim:
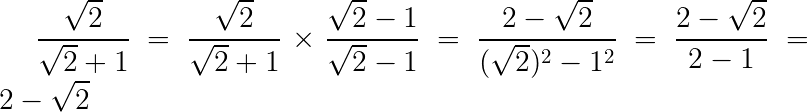
5) Racionalize o denominador da fração:

Ver resposta
Nesta questão também temos uma operação de adição no denominador. Por isso temos que multiplicar toda a fração pelo conjugado de √5 + √2, que é √5 – √2. Portanto, temos:
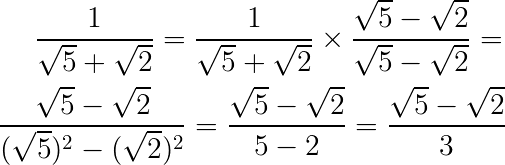
6) Racionalize a seguinte expressão:

Ver resposta
Multiplicando toda a fração pelo conjugado de √5 + 2, temos o seguinte resultado:
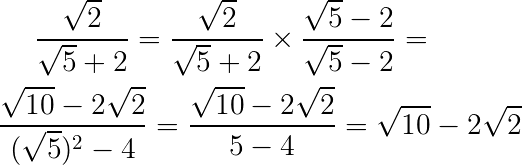
Em muitos exercícios é indispensável fazer a racionalização de denominadores, pois dessa forma nós conseguiremos resolver o problema sem afetar o resultado.
Lembre-se que o conjugado de um número é ele mesmo com o sinal invertido. Isto é, o conjugado de √5 + √2 é √5 – √2; o conjugado de √5 – 3 é √5 + 3.

