A esfera é um sólido limitado pela superfície esférica. É definida como um conjunto de pontos que distam do centro a uma mesma medida.
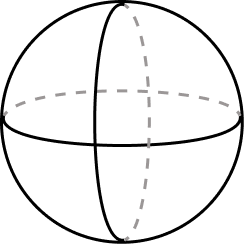
Superfície Esférica
A esfera é uma figura tridimensional, e faz parte dos estudos da geometria espacial. É um tipo de figura geométrica que podemos obtê-la através da rotação de um semicírculo em torno de seu próprio eixo.

Partes da Esfera
Ela é formada pelos seguintes elementos:
- Superfície Esférica: a superfície é formada pelos pontos que estão distantes do centro na mesma medida do raio (r);
- Cunha Esférica: a cunha esférica é a região que está entre dois semicírculos ligados ao eixo de rotação. Pode ser comparado a um gomo de uma laranja;
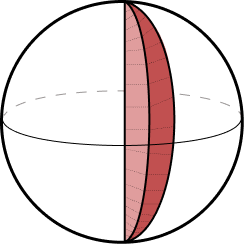
- Fuso Esférico: o fuso é uma parte da superfície da esfera que é obtida através do giro de uma semicircunferência de um ângulo entre 0 e 2π. Podemos comparar o fuso esférico como uma parte da casca de uma laranja;

- Calota Esférica: a calota é a parte da esfera cortada por um plano. Como se pegássemos uma laranja e cortasse sua parte de cima;

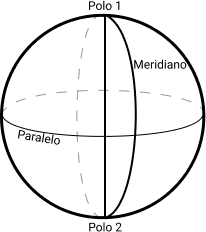
- Polos: os polos são os pontos que a superfície esférica se encontra com o eixo de rotação. Analogamente, é como os polos sul e norte da Terra;
- Paralelo: paralelo é uma circunferência na superfície esférica formada por planos perpendiculares ao eixo de rotação. O maior paralelo é chamado de Equador;
- Meridiano: é uma circunferência na superfície esférica formada por uma interseção de um plano que tem o eixo de rotação.
Área
A área é calculada através da fórmula:
A = 4 . π . r²
Onde:
- A: é a área;
- π: é o número pi (3,14);
- r: é a medida do raio.
Leia mais sobre a área da esfera
Volume
Calculamos o volume utilizando a seguinte fórmula:
V = 4⁄3 . π . r³
Onde:
- V: é a área;
- π: é o número pi (3,14);
- r: é a medida do raio.
Leia mais sobre a volume da esfera
Exercícios
Acesse os exercícios no link a seguir:

