Polígonos: Definição, Tipos e Propriedades

Polígonos são figuras geométricas fechadas que possuem muitos ângulos e lados. Os polígonos são formados por segmentos de retas unidos em pontos chamados vértices.

Euclides definiu um polígono como uma figura limitada por linhas retas, com um número de retas maior que três, numa região de um plano cercada por uma ou mais bordas.

Linha Poligonal

Uma linha poligonal é formada por segmentos de retas consecutivos que não possuem as mesmas direções. Então, a linha poligonal possui uma sequência de pontos na sua formação, de forma que em cada extremo da linha tem um ponto.

Assim, a linha poligonal formadas pelos pontos A₁A₂A₃…A_n-1A_n é igual à reunião dos segmentos de retas,

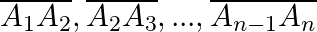
Classificação das Linhas Poligonais

As linhas poligonais são classificados como:

Linha poligonal aberta: quando os pontos extremos não são iguais;

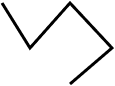
Linha poligonal fechada: quando os pontos extremos são iguais;

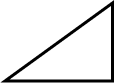
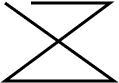
Linha poligonal simples: quando não há intersecção entre dois segmentos de retas não consecutivos;

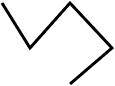
Linha poligonal não-simples: o contrário de simples.

Definição de Polígono

Um polígono é uma região no plano fechada e limitada por uma linha poligonal. Logo, definimos da seguinte forma:

Seja A₁A₂A₃…A_n-1A_n um polígono, então temos que a região poligonal é formada pelos segmentos:

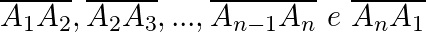
Elementos de um Polígono

Um polígono A₁A₂A₃…A_n-1A_n contém os seguintes elementos na sua formação:

• Vértice: são os extremos dos segmentos de retas que formam os lados de um polígono: A₁A₂A₃…A_n;
• Lados: os lados são formados por segmentos de retas;
• Diagonais: são segmentos de retas onde os seus extremos não são ligados em vértices consecutivos;
• Ângulo interno: os ângulos internos são formados por dois lados consecutivos;
• Ângulo externo: ângulo suplementar (a soma mede 180°) ao ângulo interno.

Exemplo:

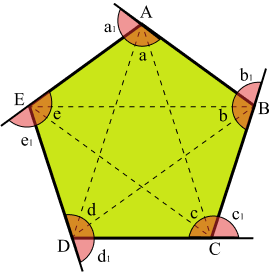
O polígono ABCDE possui:

Vértices: A, B, C, D e E;

Lados:

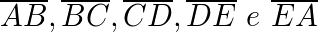
Ângulos internos:

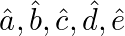
Diagonais:

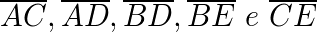
Ângulos externos:

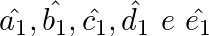
Classificação dos Polígonos

Os polígonos podem ser classificados quanto a linha poligonal, a região poligonal, a congruência e o número de lados:

• Linha poligonal: um polígono é classificado quanto a linha poligonal em:
  • Simples: quando a linha é simples, isto é, quando não há intersecção entre dois segmentos consecutivos;
  • Não-simples: quando a linha não é simples, isto é, quando há intersecções nos segmentos de retas.
• Região poligonal: a região poligonal é a parte interna limitada pelas linhas poligonais, sendo classificadas em:
  • Convexo: um polígono é convexo se dois de seus lados faz com que os outros fiquem no mesmo semiplano;
  • Não-convexo ou côncavo: quando não é convexo.
• Congruência: os polígonos congruentes são classificados em:
  • Equilátero: quando todos os lados possuem as mesmas medidas;
  • Equiângulo: quando todos os ângulos possuem as mesmas medidas;
• Número de lados: os polígonos são classificados quanto aos lados, e nomeados com as seguintes nomenclaturas:

  Lados	Nome
  1	–
  2	–
  3	triângulo
  4	quadrilátero
  5	pentágono
  6	hexágono
  7	heptágono
  8	octógono
  9	eneágono
  10	decágono
  11	undecágono
  12	dodecágono
  13	tridecágono
  14	tetradecágono
  15	pentadecágono
  16	hexadecágono
  17	heptadecágono
  18	octodecágono
  19	eneadecágono
  20	icoságono
  30	triacontágono
  40	tetracontágono
  50	pentacontágono
  60	hexacontágono
  70	heptacontágono
  80	octacontágono
  90	eneacontágono
  100	hectágono

Geralmente, nomeamos um polígono de n lados por n-látero.

Polígono Convexo

Um polígono é convexo se dois pontos A e B que formam um segmento de reta em qualquer região do polígono, o segmento de reta está contido no polígono.

Exemplo:

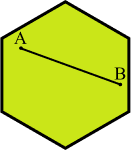
Polígono Côncavo ou não-convexo

Um polígono é côncavo se ele não for convexo, isto é, quando um segmento de reta formado por dois pontos A e B não está contido inteiramente na região poligonal.

Exemplo:

Polígono Regular

Um polígono convexo é regular quando é convexo, isto é, se o polígono for equilátero (lados com mesma medida) e equiângulo (ângulos com mesma medida).

Exemplo:

Um polígono é irregular quando os lados e os ângulos não são todos congruentes.

Propriedades

Todo polígono possui as seguintes propriedades:

• Os polígonos possuem os mesmos números de lados, ângulos e vértices;
• A soma dos ângulos internos de um polígono de n lados e convexo é dado por: S = (n – 2) . 180.
• O total de diagonais em um polígono é dado pela seguinte fórmula: d = n . (n – 3) / 2

Exercícios

Veja os exercícios no link abaixo:

• Exercícios de geometria plana