Vamos conhecer melhor o plano cartesiano resolvendo os exercícios a seguir para memorizar o conhecimento sobre o assunto.
1) Um triângulo é formato pelos pontos A(-2, 3), B(3, 1) e C(-2, 1) no plano cartesiano, calcule a área e o perímetro deste triângulo em centímetro.
Ver resposta
Identificando as coordenadas no plano cartesiano, marcando os pontos e desenhando o triângulo, temos o seguinte triângulo retângulo:
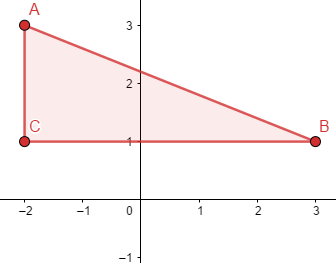
A área de um triângulo é calculada pela fórmula: A = (b . h)/2
A base é formada pelo lado BC = (3 – (-2)) = 5 cm.
A altura é formada pelo lado AC = (3 – 1) = 2 cm.
Portanto, A = (5 . 2) / 2 = 10 / 2 = 5 cm²
Para calcular o perímetro precisamos saber a medida do lado AB. Utilizando o teorema de Pitágoras, temos:
(AB)² = (AC)² + (BC)² ⇒ (AB)² = 2² + 5² ⇒ (AB)² = 4 + 25 ⇒ (AB) = √29 = 5,385 cm.
Então, o perímetro é: P = 5,385 + 5 + 2 = 12,385 cm.
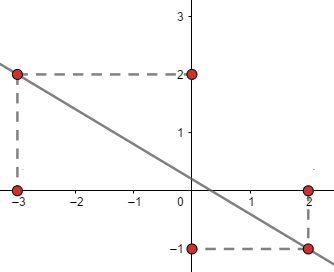
2) Identifique no plano cartesiano a reta formada pelos pontos A(2, -1) e B(-3, 2).
Ver resposta
Identificando as coordenadas e marcando os pontos no plano cartesiano, temos a seguinte reta:
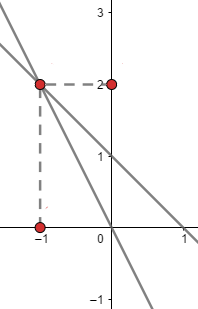
3) Determine o ponto de intersecção das retas concorrentes definidas pelas equações 2x + y = 0 e x + y – 1 = 0, indique o ponto no plano cartesiano.
Ver resposta
Isolando y em x + y – 1 = 0, temos: y = -x +1
Substituindo y em 2x + y = 0, temos: 2x + (-x + 1) = 0 ⇒ x + 1 = 0 ⇒ x = -1
Substituindo x = -1, em y = -x + 1, temos: y = -(-1) + 1 ⇒ y = 2
Portanto, o ponto de intersecção das retas é: (-1, 2)
Identificando no plano cartesiano:
Então é isso, praticando estes exercícios fica tranquilo entender sobre o plano cartesiano.


