Responda os exercícios a seguir de sequência numérica e após a resolução de cada questão verifique a resposta da questão para conferir a sua resposta.
1) Determine os três próximos números da sequência 0, 5, 10, 15, 20, …
Ver resposta
Perceba que temos uma PA com razão 5.
Portanto, podemos continuar desenvolvendo a sequência utilizando a fórmula do termo geral da PA.
an = a1 + (n – 1) . r
Assim, os três próximos termos são:
a6 = 0 + (6 – 1) . 5 = 0 + 5 . 5 = 25
a7 = 0 + (7 – 1) . 5 = 0 + 6 . 5 = 30
a8 = 0 + (8 – 1) . 5 = 0 + 7 . 5 = 35
Portanto, os três próximos termos da sequência são: 25, 30 e 35
0, 5, 10, 15, 20, 25, 30, 35, …
2) Escreve por extenso parte da sequência definida pela fórmula n² + 1, n ∈ N.
Ver resposta
Atribuindo números naturais a n, temos:
n = 0: 0² + 1 = 1
n = 1: 1² + 1 = 2
n = 2: 2² + 1 = 4 + 1 = 5
n = 3: 3² + 1 = 9 + 1 = 10
n = 4: 4² + 1 = 16 + 1 = 17
n = 5: 5² + 1 = 25 + 1 = 26
n = 6: 6² + 1 = 36 + 1 = 37
n = 7: 7² + 1 = 49 + 1 = 50
n = 8: 8² + 1 = 64 + 1 = 65
n = 9: 9² + 1 = 81 + 1 = 82
n = 10: 10² + 1 = 100 + 1 = 101
Então, temos parte da sequência: 1, 2, 5, 10, 17, 26, 37, 50, 65, 82, 101, …
3) Determine a soma dos dois próximos termos da sequência com ordem lógica 0, 2, 6, 2, 4, 12, 4, 6, 18, 6, …
Ver resposta
Veja que a sequência é formada pelos múltiplos de 6 e de 2.
Múltiplos de 2 repetidos: _, 2, _, 2, 4, _, 4, 6, _, 6
Múltiplos de 6: _, _, 6, _, _, 12, _, _, 18, _, …
Então, podemos continuar a sequência:
0, 2, 6, 2, 4, 12, 4, 6, 18, 6, 8, 24, 8, 10, 30, 10, …
Os dois próximos números da sequência da questão são 8 e 24. Portanto,
24 + 8 = 32
4) Determine o décimo termo desta PG: 1, 6, 36, 216, 1296, …
Ver resposta
Para encontrarmos um termo qualquer de uma PG, utilizamos a fórmula do termo geral.
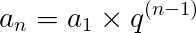
Primeiro temos que calcular a razão desta PG. Para isso, podemos pegar qualquer termo e dividi-lo pelo seu antecessor na sequência, assim, temos que a razão desta PG é: 6, pois 36/6 = 6
Portanto, temos: