O Teorema de Tales diz que se duas retas são transversais a um feixe de retas paralelas, então a razão entre as medidas de dois segmentos quaisquer de uma delas é igual à razão entre as medidas dos segmentos correspondentes da outra.
Esse teorema foi desenvolvido pelo filósofo, matemático e astrônomo grego Tales de Mileto.
Tales observou os raios solares que chegavam à terra de forma inclinada e paralelos, então ele chegou a conclusão de que havia uma proporção entre as sombras e a altura dos objetos.
Dessa forma, ao observar a pirâmide de Quéops no Egito, ele conseguiu calcular a altura da pirâmide de acordo com o tamanho da sombra projetada por ela.
Para calcular a altura da pirâmide, Tales fincou uma estaca e mediu o tamanho da sombra da pirâmide e da estaca. Como podemos ver na figura a seguir:

Assim, ele estabeleceu a seguinte proporção:
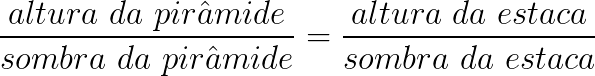
Tal estudo é utilizado hoje no cálculo de distâncias através da razão e proporção.
O Teorema Aplicado nas retas
Se tivermos um feixe de retas paralelas entre si, cortadas por duas transversais, segmentos proporcionais são formados pela intersecção entre as retas paralelas e as transversais.
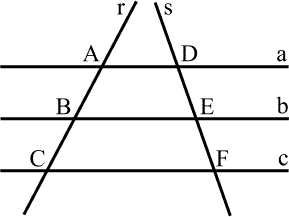
Pela imagem, os seguintes segmentos são proporcionais:
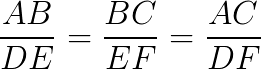
O Teorema de Tales no Plano
Esse teorema aplicado no plano diz que se tivermos um feixe de planos paralelos cortado por duas transversais, determina segmentos correspondentes proporcionais.
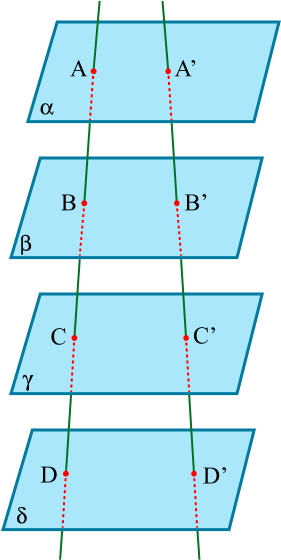
Como os planos são paralelos entre si, os seguintes segmentos formados pelas retas transversais que cortam os planos, são proporcionais. Então:
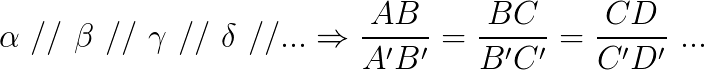
Teorema de Tales nos Triângulos
O Teorema de Tales também pode ser aplicado nos triângulos. Se traçarmos uma reta paralela a um dos lados, cortando o triângulo ao meio, temos que os segmentos formados entre os lados do triângulo e a reta são proporcionais aos lados originais do triângulo.
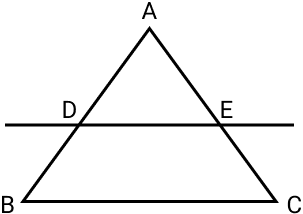
Dessa forma, é correto afirmar que de acordo com a semelhança de triângulo, o triângulo formado pela reta paralela a um dos lados é semelhante ao triângulo original. Então:
Δ ABC ~ Δ ADE
Exercícios
Acesse os exercícios no link a seguir:
Bons estudos!

