Probabilidade é uma área de estudo na matemática que permite calcular as chances de um evento ocorrer em um experimento aleatório.
Existem dois tipos de fenômenos estudados: os fenômenos determinísticos e os aleatórios.
- Fenômenos determinísticos: são aqueles em que os resultados podem ser previstos antes da sua realização;
- Fenômenos aleatórios: são aqueles em que os resultados não podem ser previstos, mesmo que seja repetido em condição idêntica para todos os experimentos realizados.
Fórmula da Probabilidade
A probabilidade de uma evento ocorrer em um número de casos possíveis pode ser calculada pela seguinte fórmula:
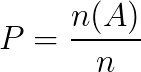
Onde:
- P: é a probabilidade;
- n(A): número de eventos favoráveis;
- n: total de eventos possíveis.
Experimento Aleatório
Um experimento aleatório depende apenas do acaso. Isto quer dizer que não podemos prever o que vai ocorrer no experimento, mesmo que as condições de realização do evento sejam as mesmas em todos os casos.
Por exemplo, o lançamento de uma moeda no ar. Existem duas probabilidades de um evento ocorrer: cara ou coroa. Porém, não podemos dizer qual lado da moeda vai cair virado para cima. Em todos os lançamentos, a moeda é jogada nas mesmas condições.
Exemplos:
- Lançar um dado e verificar o número da face que caiu virado para cima;
- Lançar uma moeda e verificar se foi cara ou coroa;
- Retirar uma carta do baralho e verificar qual foi o naipe obtido.
Espaço Amostral e Evento
O espaço amostral é o conjunto de todos os resultados possíveis que um evento pode ocorrer em um experimento aleatório. Para representar o espaço amostral, vamos identificá-lo com a letra U.
O evento é qualquer subconjunto do espaço amostral. O indicaremos com a letra A.
Exemplo:
- Experimento: considere um conjunto formado pela ocorrência de um número par no naipe
de paus.
- Espaço amostral:
- U = {A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K}
- Evento:
- A = {2, 4, 6, 8, 10}
- Espaço amostral:
- Experimento: lançar uma moeda no ar e verificar a face que caiu virado para
cima.
- Espaço amostral:
- U = {cara, coroa}
- Evento:
- A = {cara ou coroa}
- Espaço amostral:
Evento Complementar
Considere U como um espaço amostral finito e não vazio e A um evento de U. O evento complementar de A, ou seja, os eventos que não pertencem a A, é indicado por:
Notação para Evento Complementar:
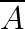
Exemplo:
Seja A = {1; 3; 5} um evento da possibilidade de sair um número ímpar no lançamento de um dado. Assim,
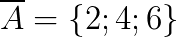
Analogamente, é igual ao que estudamos na teoria dos conjuntos sobre o complementar de um conjunto.
Veja como fica esquematicamente na imagem a seguir:
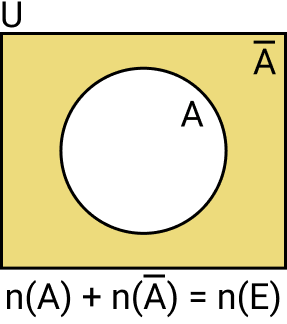
O número de eventos favoráveis mais o número de eventos complementares (não favoráveis) é igual ao conjunto de eventos possíveis.
Probabilidade de Ocorrência de um Evento
Um experimento aleatório em um espaço amostral U, tal que n(U) é o número de elementos de U. Considere A o conjunto de eventos de U, e n(A) o total de elementos desse conjunto.
Definimos a probabilidade de um evento A ocorrer por:
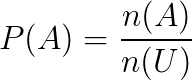
Onde:
- P(A): probabilidade de um evento A ocorrer;
- n(A): número total de ocorrências do evento A;
- n(U): número de ocorrências no espaço amostral.
Exemplo:
Considere um baralho, então:
- n(U) = 52 (total de cartas no baralho);
- n(A) = 5 (total de cartas pares de paus).
Assim, a probabilidade de alguém pegar uma carta par do naipe de paus é de:
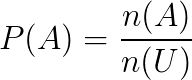
P(A) = 5/52 = 0,096
Isto quer dizer que a probabilidade de uma pessoa pegar um naipe par de paus é de, aproximadamente, 9,6%.
União de Dois Eventos
Se tivermos dois eventos A e B de um espaço amostral U, como mostra a figura a seguir:
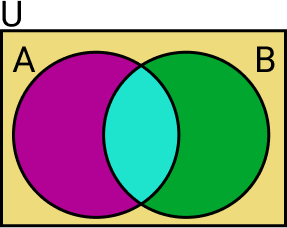
O número de elementos da união de A e B é:
- n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Então, se dividirmos os dois lados por n(U), temos que:
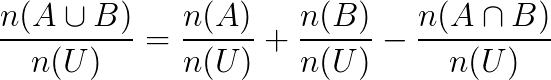
Assim,
- P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Quer dizer que a probabilidade de ocorrer um evento de A ou B, é a probabilidade de ocorrer os eventos de A mais os eventos de B, excluindo os eventos que pertencem A e B ao mesmo tempo, a interseção.
Se A e B forem dois eventos mutuamente exclusivos, isto é, A ∩ B = ∅. Então, a probabilidade de eventos de A e B ocorrerem ao mesmo tempo é nula (P(A ∩ B) = ∅), temos então neste caso,
- P(A ∪ B) = P(A) + P(B)
Propriedades da Probabilidade
A probabilidade possui as seguintes propriedades:
P(U) = 1
P(∅) = 0
0 ≤ P(A) ≤ 1
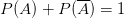
Exercícios
Veja os exercícios acessando o link abaixo:


