O plano cartesiano é um sistema criado pelo matemático René Descartes. O sistema é constituído de dois eixos, x e y, sendo perpendiculares entre si, ou seja, os eixos se cruzam formando um ângulo reto (ângulo que mede 90°).
O eixo x é chamado eixo das abscissas e o eixo y é chamado eixo das ordenadas.
Os dois eixos x e y dividem o plano cartesiano em 4 (quatro) quadrantes. Um ponto no plano cartesiano é a associação de um valor do eixo x e outro do eixo y, esse ponto é chamado par ordenado (x, y)
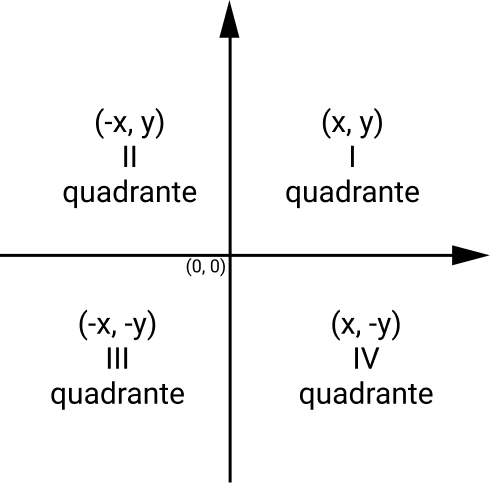
Construção do sistema de coordenadas cartesianas
Para construir um plano cartesiano devemos traçar duas retas perpendiculares entre si.
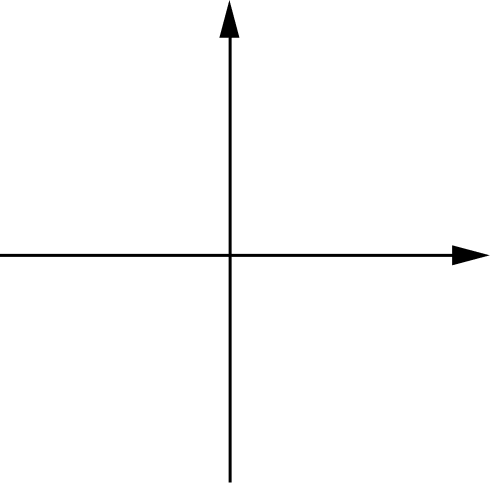
A reta horizontal deve ser identificada como a reta x, chamada eixo x ou eixo das abscissas. A reta vertical deve ser identificada como a reta y, chamada eixo y ou eixo das ordenadas.
Além disso, o ponto onde as retas se cruzam é o ponto de origem, o par ordenado (0, 0). Antes da origem, os eixos devem ser numerados com números negativos e depois da origem com números positivos. Veja com fica:

Localizando um ponto no Plano Cartesiano
A localização de um ponto no plano cartesiano formado pelo par ordenado (x, y), deve ser feita da seguinte maneira:
- Localizar o valor para x no eixo das abcissas;
- Localizar o valor para y no eixo das ordenadas;
- O ponto é onde o par ordenado (x, y) se encontra.
Exemplo:
Localizar no plano cartesiano os pontos formados pelos pares ordenados (2, 5), (3, -1), (-2, -2) e (-5, 4):
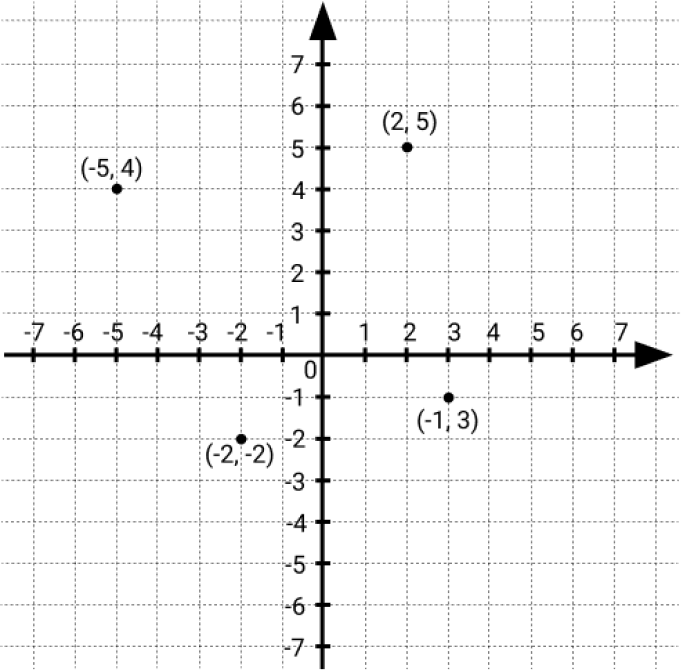
Estude o plano acima e entenda o funcionamento.
Produto cartesiano
O produto cartesiano é a multiplicação entre os pares ordenados (x, y) onde x ∈ A e y ∈ B, sendo A e B conjuntos. O produto cartesiano foi criado também por René Descartes e é amplamente usado na teoria dos conjuntos.
Definição:
Sejam os conjuntos A e B, não-vazios, chamamos produto cartesiano A x B, o conjunto dos pares ordenados (x, y), onde x ∈ A e y ∈ B. Assim:
A x B = {(x, y) | x ∈ A e y ∈ B}
Exemplo:
Considere os conjuntos: A = {1, 2} e B = {2, 4}
Os conjuntos dos pares ordenados de A e B é: A x B = {(1, 2), (1, 4), (2, 2), (2, 4)}; o diagrama de flechas abaixo mostra essa relação do produto A x B. Veja:
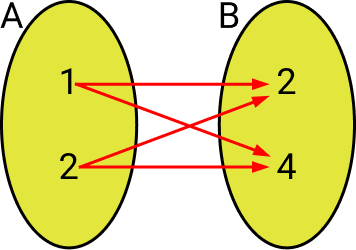
Exercícios
Acesse os exercícios no link a seguir:


