A função quadrática é uma função polinomial do 2º grau. A função quadrática tem a seguinte lei de formação: f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0.
Exemplos de funções quadráticas:
- f(x) = 2x² – 2x + 1, com a = 2, b = -2 e c = 1
- f(x) = x² + x – 2, com a = 1, b = 1 e c = -2
- f(x) = 5x² + 3x + 3, com a = 5, b = 3 e c = 3
Índice do Artigo
Definição
É uma função f: R → R definida por f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0.
Essa é a definição da função quadrática ou função polinomial do 2º grau. Por causa do grau 2, a função possui um gráfico curvo que é chamado de parábola.
Resolução de uma Função Quadrática
Seja a função f(x) = 2x² – 3x + 1, encontre as raízes da função e esboce o gráfico.
Vamos resolver essa questão usando a fórmula de Bhaskara.
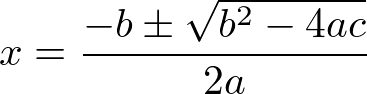
Raízes da Função
Vamos separar os coeficientes: f(x) = 2x² – 3x + 1
- a = 2
- b = -3
- c = 1
Substituindo na fórmula de Bhaskara, temos:
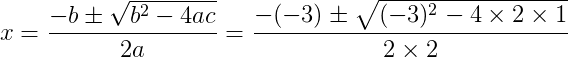
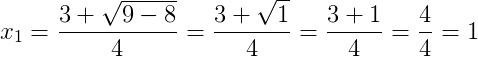
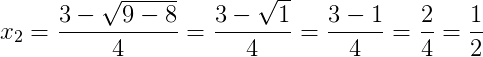
Assim, as raízes da função são 1 e 1⁄2.
As raízes da função depende do discriminante: Δ = b² – 4ac
Portanto, temos as seguintes condições:
- Se Δ > 0, a função possui duas raízes reais e distintas (x1 ≠ x2);
- Se Δ < 0, a função não possui raízes reais;
- Se Δ = 0, a função possui duas raízes reais e iguais (x1 = x2).
Gráfico da Função Quadrática
O gráfico da função quadrática é uma curva que chamamos de parábola. A necessidade de encontrarmos as raízes da função é que o gráfico deve passar pelos pontos que representam as raízes.
A orientação do gráfico depende do coeficiente a. Assim,
- Se a > 0, o gráfico possui uma parábola com concavidade para cima;
- Se a < 0, o gráfico possui uma parábola com concavidade para baixo.
Interseção com o eixo Oy
O gráfico cortará o eixo das ordenas (eixo y) no valor do coeficiente c, na função acima o valor de c = 1, portanto o gráfico intercepta o eixo y no ponto 1.
Raízes
As raízes encontradas acima também devem estar no gráfico, dessa forma as raízes são os dois pontos do eixo das abcissas (eixo x) onde o gráfico intercepta no eixo x.
Vértice do gráfico
O vértice do gráfico é dado pelas seguintes fórmula:
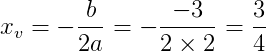
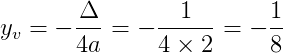
Para a fórmula acima precisamos calcular o Δ.
- Δ = b² – 4ac = (-3)² – 4 . 2 . 1 = 9 – 8 = 1
Logo, V = (xv, yv) = (3⁄4, –1⁄8)
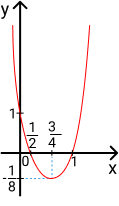
Esboço do gráfico
Com os valores acima podemos desenhar o gráfico da função.
Encontrou algum erro? Nos avise clicando aqui
by