Treine os seus conhecimentos sobre a aplicação do teorema de Tales resolvendo os exercícios a seguir.
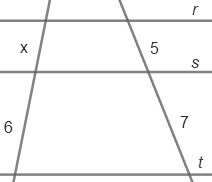
1) Sabendo que r // s // t, determine o valor de x.
Ver resposta
Sabendo que x e 5 são medidas correspondentes localizadas entre as retas r e s, e 6 e 7 também são correspondentes localizadas entre as retas s e t, então podemos montar a proporção:
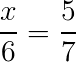
Fazendo a multiplicação cruzada da proporção, temos o seguinte:
7x = 6 . 5 ⇒
7x = 30 ⇒
x = 30/7 ⇒
x = 4,3
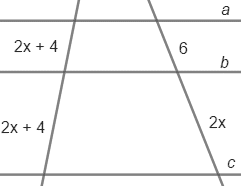
2) Sabendo que a // b // c, calcule o valor x:
Ver resposta
Aplicando o teorema de Tales, temos a seguinte proporção:
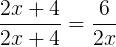
Multiplicando em cruz, temos que:
2x(2x + 4) = 6(2x + 4) ⇒
4x² + 8x = 12x + 24 ⇒
4x² + 8x – 12x – 24 = 0 ⇒
4x² – 4x – 24 = 0
Temos uma equação do segundo grau com:
a = 4, b = – 4 e c = -24
Δ = b² – 4 . a . c = (-4)² – 4 . 4 . (-24) = 16 + 384 = 400
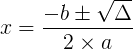
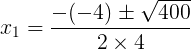
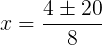
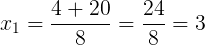
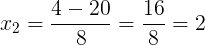
O número 2 não é interessante, pois ao substituir na proporção não temos uma igualdade. Já o número 3, sim.
Portanto, o valor de x é 3.
3) (FUVEST-SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180 m?
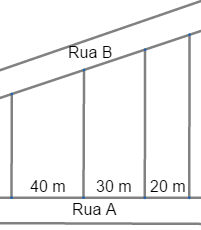
Ver resposta
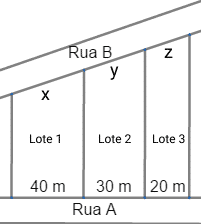
Observando a imagem acima e aplicando o teorema de Tales, temos o seguinte:
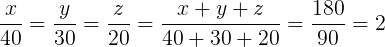
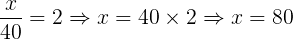
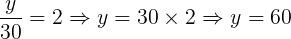
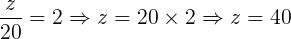
Portanto, cada lote possui as seguintes medidas de frente:
Lote 1 = 80 m
Lote 2 = 60 m
Lote 3 = 40 m
O teorema de Tales é muito importante para resolver diversos exercícios, portanto é imprescindível estudá-lo.

