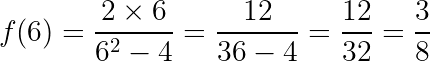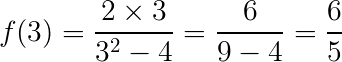Testes seus conhecimentos sobre função respondendo os exercícios a seguir.
1) Seja f uma função dada por f(x) = ax + b, sendo a e b números reais. Determine o valor de f(5) sabendo que f(-1) = 1 e f(1) = 2.
Ver resposta
f(x) = ax + b ⇒
f(-1) = 1 ⇒
f(-1) = a . (-1) + b ⇒
1 = – a + b
f(1) = 2 ⇒
f(1) = a . 1 + b ⇒
2 = a + b ⇒
Fazendo um sistema de equações, temos:
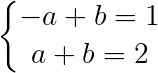
Vamos isolar a na primeira equação:
– a + b = 1 ⇒
a = b – 1
Substituindo a na segunda equação, temos:
a + b = 2 ⇒
(b – 1) + b = 2 ⇒
2b – 1 = 2 ⇒
2b = 2 + 1 ⇒
b = 3/2
Vamos substituir b na primeira equação:
– a + b = 1 ⇒
– a + 3/2 = 1 ⇒
– a = 1 – 3/2 ⇒
– a = – 1/2 ⇒
a = 1/2
Então temos que a função será f(x) = 1/2 . x + 3/2.
Portanto, o valor de f(5) = 1/2 . 5 + 3/2 = 5/2 + 3/2 = 8/2 = 4
2) Considere a função f(x) = 31x + 25, calcule o valor de f(32) e f(43).
Ver resposta
Basta substituirmos os valores de x na função: f(x) = 31x + 25
Assim:
f(32) = 31 . 32 + 25 = 1017
f(43) = 31 . 43 + 25 = 1358
3) Seja uma função f definida por f(x) = 4x – 21, determine f(10) + f(2) e f(3) * f(5).
Ver resposta
Primeiro devemos substituir os valores de x e depois realizar as operações:
f(10) = 4 . 10 – 21 = 40 – 21 = 19
f(2) = 4 . 2 – 21 = 8 – 21 = – 13
Logo, f(10) + f(2) = 19 + (-13) = 6
f(3) = 4 . 3 – 21 = – 9
f(5) = 4 . 5 – 21 = 20 – 21 = – 1
Portanto, f(3) * f(5) = (-9) * (-1) = 9
4) Seja uma função definida pela expressão f(x) = mx + n, se o gráfico da função f passa pelos pontos (2, 5) e (-1, 2), determine o valor de m.
Ver resposta
Temos que o primeiro ponto no gráfico é (2, 5), dessa forma o valor de x é 2, e f(2) = 5.
Se substituirmos na expressão f(x) = mx + n, temos:
f(2) = m . 2 + n ⇒
5 = m . 2 + n ⇒
n = – 2m + 5
Substituindo também os valores do segundo ponto (-1, 2), x = -1 e f(x) = 2, teremos:
f(x) = mx + n ⇒
f(-1) = m . (-1) + n ⇒
2 = – m + n ⇒
n = m + 2
Encontramos dois valores para n, assim igualando temos:
– 2m + 5 = m + 2 ⇒
m + 2m = 5 – 2 ⇒
3m = 3 ⇒
m = 1
5) Determine o domínio da função:
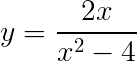
Determine também as imagens para x = 6 e x = 3.
Ver resposta
Nesta função o denominador não pode ser igual a zero. Assim:
x² – 4 = 0 ⇒
(x – 2)(x + 2) = 0 ⇒
x ≠ (-2, 2)
O domínio da função é: D = {x ∈ R | x ≠ -2 e x ≠ 2}
Para encontrar as imagens da função solicitadas nos exercícios, vamos substituir os valores de x dados: