A probabilidade condicional é um conceito da probabilidade que envolve dois eventos de forma que estuda a probabilidade de o evento A ocorrer, sabendo que o evento B já ocorreu.
Considere dois eventos A e B em um espaço amostral U, não vazio. A probabilidade de A condicionada a B, ou seja, a probabilidade de A ocorrer sabendo que B já ocorreu, é dado por:

Exemplo:
Numa aula de dança existem 50 alunos, 15 homens e 35 mulheres. Sabendo que 10 homens e 15 mulheres foram selecionados para uma apresentação. Uma pessoa é sorteada ao acaso.
Qual a probabilidade de:
- Ela ser do sexo feminino se foi sorteada para a apresentação?
- Ela ter sido sorteada se é do sexo masculino?
Resolução:
A tabela abaixo mostra os dados do problema:
| Sorteada | Não sorteada | Total | |
|---|---|---|---|
| Homem | 10 | 5 | 15 |
| Mulher | 15 | 20 | 35 |
| Total | 25 | 25 | 50 |
Evento A: “a pessoa foi sorteada para a apresentação de dança”.
Evento B: “a pessoa sorteada é mulher”.

Evento A: “a pessoa foi sorteada para a apresentação de dança”.
Evento C: “a pessoa sorteada é homem”.
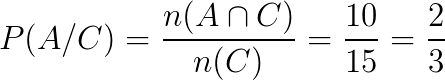
Eventos Independentes
Seja dois eventos A e B em um espaço amostral U, então dizemos que os eventos A e B são independentes, se a ocorrência no evento A não modificar a ocorrência no evento B.
Logo,
A e B são independentes ⇔ P(B | A) = P(B) e P(A | B) = P(A)
Quando os eventos A e B são independentes temos que:
- P(A ∩ B) = P(A) · P(B)
Dessa forma, caso P(A ∩ B) ≠ P(A) · P(B), então os eventos A e B são dependentes.
Exemplo de eventos independentes
Quando tiramos duas cartas de um baralho, e depois que tirarmos uma segunda carta, a primeira carta já estiver de volta no baralho, o resultado da primeira carta não influenciará no resultado da segunda carta.
Exemplo de eventos dependentes:
Quando tiramos duas cartas de um baralho, e depois formos tirar a segunda carta e não colocamos de volta a primeira, o resultado da primeira influenciará no resultado da segunda carta, pois temos um espaço amostral diferente para a segunda carta que passa a ter 51 cartas e não 52 cartas.
Exemplo:
Considere uma urna contendo 50 bolas, destas 50 bolas, 20 são azuis e 30 vermelhas. Sorteando 1 bola de cada vez, toda vez a bola sorteada é reposta na urna. Qual é a probabilidade da primeira bola sorteada ser azul e a segunda ser vermelha?
Resolução:
Temos um problema com eventos independentes. A probabilidade de retirar uma bola azul na primeira vez e uma vermelha na segunda vez é o produto de cada evento ocorrer: P(A ∩ B) = P(A) · P(B)
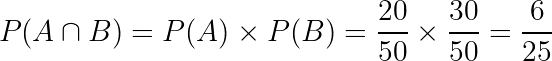
Intersecção de Eventos
Seja dois eventos A e B em um espaço amostral U. Então, dizemos que o evento A ∩ B é a ocorrência de A e B ao mesmo tempo.
No cálculo de eventos simultâneos, utilizamos a seguinte fórmula da probabilidade condicional:
- P(A ∩ B) = P(A) . P(B/A) = P(B) . P(A/B)
Exemplo:
Considere um globo em um bingo onde possui 75 bolas numeradas de 1 a 75. Qual a probabilidade de retirarmos a bola 10 e, sem reposição, a bola 5?
Resolução:
A probabilidade retirar a bola 10 é:
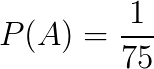
Agora a urna possui 74 bolas, assim a probabilidade de retirarmos a bola 5, tendo retirado a bola 10 na primeira retirada, é:
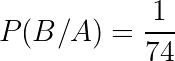
Por fim, queremos saber qual a probabilidade de os dois eventos ocorrerem simultaneamente. Então, temos que:
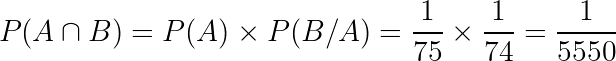
Propriedades da Probabilidade Condicional
- A e B independentes ⇔ P(A ∩ B) = P(A) . P(B);
- A e B dependentes ⇔ P(A ∩ B) ≠ P(A) . P(B);
- Se A e B são independentes, então temos que P(B/A) = P(B) e P(A ∩ B) = P(A) . P(B).
Exercícios
Acesse os exercícios no link a seguir:


