Responda os exercícios sobre o trapézio a seguir para ajudar a compreender como aplicar as fórmulas estudadas.
1) Determine a área do trapézio com bases maior e menor medindo, respectivamente, 6 cm e 4 cm, e altura de 9 cm.
Ver resposta
Vamos aplicar a fórmula e verificar o resultado: A = ((B + b) x h)/2
Então: A = ((6 + 4) x 9)/2 = (10 x 9)/2 = 90/2 = 45
Portanto, a área do trapézio é 45 cm².
2) Considere um trapézio isósceles com lados medindo 5 cm, base maior 6 cm e menor de 2 cm, e altura, 8 cm. Calcule:
a) área
b) perímetro
c) mediana
d) a área da mediana
Ver resposta
a) A área é calculada pela fórmula: A = ((B + b) x h)/2
Logo: A = ((6 + 2) x 8)/2 = (8 x 8)/2 = 64/2 = 32
Então a área é igual a 32 cm²
b) O perímetro do trapézio é calculado pela seguinte fórmula: P = B + b + L1 + L2
Então: P = 6 + 2 + 5 + 5 = 18
O perímetro é igual a 18 cm.
c) A mediana é calculada pela fórmula: m = (B + b)/2
Assim: m = (6 + 2)/2 = 8/2 = 4
Logo, a mediana mede 4 cm.
d) A área da mediana é calculada pela fórmula: A = m x h
Então: A = 4 x 8 = 32 cm
Logo, a área da mediana é: 32 cm²
3) Sabendo que um trapézio retângulo com as seguintes medidas: base maior, 5 cm; base menor, 4 cm; e altura de 6 cm. Calcule a média de pelo menos um dos lados.
Ver resposta
A medida de um dos lados de um trapézio retângulo é a própria altura. A medida do outro lado é calculada pela fórmula:
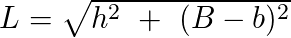
Logo,
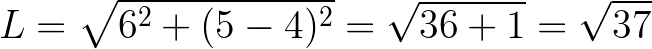
Portanto, a medida de um dos lados do trapézio retângulo é igual a √37 cm. Ou aproximadamente 6,1 cm.
Bom, estes exercícios sobre o trapézio são suficientes para praticar e memorizar a fórmula.

