Responda os exercícios a seguir sobre o volume da esfera para entender e memorizar as fórmulas.
1) Determine o volume de uma esfera cujo raio mede 5 cm.
Ver resposta
O volume da esfera é calculado pela seguinte fórmula: V = 4/3 . π . r³
Então, o volume é: V = 4/3 x 3,14159 x 5³ = 523,6 cm³
2) Calcule a medida do raio de uma bola de futebol cujo volume é igual a 300 cm³
Ver resposta
Sabemos que o volume é calculado por: V = 4/3 . π . r³
Assim, temos que:
V = 4/3 . π . r³ ⇒ 300 = 4/3 x 3,14159 x r³ ⇒ 300 = 4,19r³ ⇒ r³ = 300/4,19
⇒ 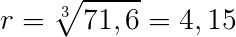
3) Seja uma esfera com raio de 6 cm, calcule:
a) Volume da esfera;
b) Volume da cunha esférica com ângulo de 90°;
c) Volume do setor esférico com altura de 4 cm;
d) Volume do setor esférico de uma base com altura de 2 cm;
e) Volume do setor esférico de duas bases com altura de 8 cm e raio da base 1 e 2 de 4 cm.
Ver resposta
a) O volume da esfera é calculado pela seguinte fórmula: V = 4/3 . π . r³
Então, o volume desta esfera é: V = 4/3 . π . 6³ = 904,79 cm³
b) O volume da cunha é calculado pela fórmula: Vc = (π . r³ . α°)/270°
Logo: Vc = (π . 6³ . 90)/270 = 61072,5 / 270 = 226,19 cm³
c) O volume do setor esférico é calculado pela fórmula: Vse = 2/3 . π . r² . h
Assim: Vse = 2/3 . π . 6² . 4 = 301,59 cm³
d) O volume do setor esférico de uma base é calculado pela seguinte fórmula: Vse1b = (π . h)/6 . (3 . r² . h²)
Então: Vse1b = (3,14159 x 2)/6 x (3 x 6² x 2²) = 452,39 cm³
e) O volume do setor esférico de duas bases é calculado pela fórmula: Vse2b = (π . h)/6 . [3 . (r1² + r2²) + h²]
Dessa forma, temos que o volume é:
Vse2b = (π x 8)/6 x [3 . (4² + 4²) + 8²] = 4,19 x [3 x 32 + 64] = 4,19 x [96 + 64] = 4,19 x 160 = 670,4 cm³
Veja também:

