Preparamos alguns exercícios sobre os números reais para praticar e entender operações envolvendo os elementos deste conjunto.
1) Responda às afirmações a seguir se são verdadeiras ou falsas:
a) O conjunto dos números naturais (N) é subconjunto dos reais (R);
b) O resultado de 2 + √3 é um número real;
c) O conjunto dos inteiros (Z) pertence ao conjunto dos reais (R) ;
d) Se um elemento pertence ao conjunto dos números irracionais (I), então ele também pertence ao conjunto dos reais (R);
e) Q ⊂ R
Ver resposta
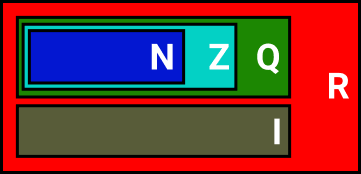
a) Um conjunto A é subconjunto de B quando os elementos de A são elementos também de B, ou seja, A ⊂ B. Então, como podemos ver pelo diagrama abaixo, os elementos de N ⊂ R. Portanto, a afirmação é verdadeira.
b) O número 2 é um número inteiro e √3 é irracional, dessa forma, como a somamos um inteiro com um irracional e estes conjuntos são subconjuntos de R, então o resultado também será um número real. Verdadeira.
c) Falso, a relação de pertinência é utilizado para elementos de um conjuntos.
d) Verdade, como o conjunto dos irracionais é subconjunto dos reais, então qualquer elemento de I será também elemento de R.
e) Verdade, o conjunto dos racionais está contido no conjunto dos reais, ou seja, Q é subconjunto de R.
2) Considere o conjunto: A = {23, 1,333333…, 1/2, √5, -34, √64}; identifique a qual conjunto os elementos de A pertencem.
Ver resposta
23 é um número natural e também um inteiro;
1,333333… é um número racional pois é o resultado da fração 4/3;
1/2 é um número racional;
√5 pertence aos irracionais;
-34 é um número inteiro;
√64 é um número natural e também um inteiro, pois √64 = 8;
Todos os números do conjunto A são números reais.
3) Representas as frações a seguir na forma decimal:
a) 6/5
b) 4/7
c) 2/3
d) 7/2
e) 3/9
Ver resposta
a) 1,2
b) 0,571428…
c) 0,66666…
d) 3,5
e) 0,333333…


