Os ângulos complementares são os ângulos cuja soma equivale a 90°. Esses ângulos estão compreendidos entre 0° e 90°.
Dois ângulos complementares que compartilham um mesmo lado e um vértice entre eles, são chamados de adjacentes.
Além disso, não existem pontos que são comuns a região compreendida dos ângulos adjacentes.

Os ângulos AÔC e BÔC são complementares e adjacentes cuja soma é 90°.
Como Calcular?
Para sabermos se dois ângulos são complementares precisamos apenas verificar se a soma das duas medidas é igual a 90°.
Exemplo:
- A = 30°
- B = 60°
- 30° + 60° = 90°
A e B são complementares.
Para acharmos o ângulo complementar de um ângulo basta subtrair a medida desse ângulo por 90°.
Assim:
- A + B = 90°
- B = 90° – A
Analogamente,
- A = 90° – B
Exemplo:
Seja os ângulos A e B, com A = 20° e B com medida desconhecida.
Então:
- B = 90° – A = 90° – 20° = 70°
Assim, B = 70°
Diferença entre Ângulos Complementares, Suplementares e Replementares
Os ângulos complementares são os ângulos que a soma das medidas dos dois ângulos equivale a 90°. Enquanto que os ângulos suplementares a soma das medidas dos ângulos equivale a 180°. Já os ângulos replementares, a soma das medidas equivale a 360°.
Ângulos Adjacentes
Dois ângulos são adjacentes quando eles compartilham um lado em comum, um vértice e a região de cada ângulo não tenha pontos em comum.
Os ângulos adjacentes podem ser complementares, quando a soma é igual a 90°, e também podem ser suplementares, quando a soma equivale a 180°.
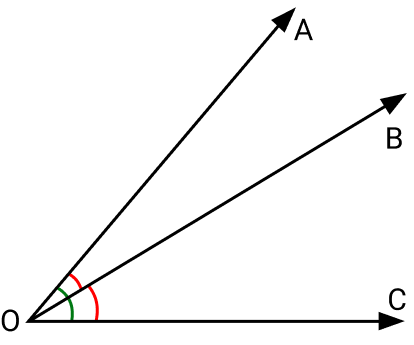
Na imagem acima, os ângulos AÔB e BÔC são adjacentes, pois além de possuir o lado OB e o vértice O em comum, as regiões internas de cada ângulos não possuem pontos compartilhados.
Da mesma forma podemos afirmar que os ângulos AÔC e AÔB não são adjacentes, mesmo possuindo o lado OC e o vértice O em comum. No entanto, a região do ângulo AÔB possui pontos compartilhados com o ângulo AÔC.
Como medir ângulos?
Para medir qualquer ângulo, utilizamos o auxílio de uma ferramenta chamada de transferidor.

Posicione a base do transferidor correspondente ao ângulo 0 sobre um dos lados do ângulo, agora verifique o outro lado do ângulo. A medida que estiver sobre o outro lado do ângulo é a medida do ângulo medido.
Com o transferidor, que pode ser encontrado facilmente em papelarias, conseguimos medir qualquer ângulo.



