Razão e proporção são utilizadas para realizar comparações ou estabelecer igualdade entre grandezas diferentes. Dessa forma, a razão realiza a comparação enquanto a proporção faz a igualdade.
Razão
Usamos razão para fazer comparação entre duas grandezas. Assim, quando dividimos uma grandeza pela outra estamos comparando a primeira com a segunda.
Definição:
Sabendo que existe duas grandezas a e b, a razão entre a e b, com b diferente de zero, é o quociente entre a e b: a:b ou

Exemplo:
Seja a = 18 e b = 12, qual a razão entre a e b?
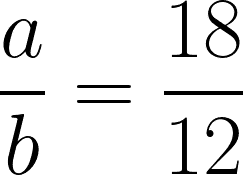
mas
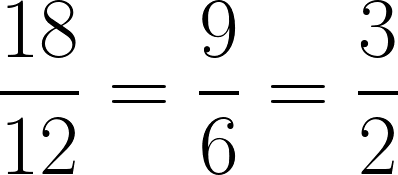
que são todas razões equivalentes.
Primeiro, dividimos por 2, o menor número possível (com exceção do 0 e 1), o numerador e o denominador. Depois dividimos por 3 o resultado da divisão anterior, que era o mínimo possível que podíamos dividir tanto o numerador quanto o denominador.
Assim, podemos dizer que a:b = 3:2 ou

Veja exercícios sobre razão, aqui.
Proporção
Proporção é a igualdade entre duas razões (equivalências entre razões). Ou seja, se dissermos que as razões
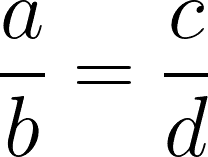
são iguais, é o mesmo que dizer que elas formam uma proporção.
Propriedade fundamental da proporção
O produto dos meios é igual aos produtos dos extremos.
Então, ao escrevermos
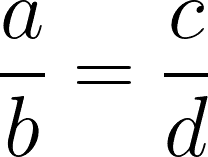
dizemos que a e d são os extremos da proporção e b e c são os meios da proporção.
Considerando o conjunto dos números reais, podemos concluir algumas equivalências entre as proporções. Portanto, para
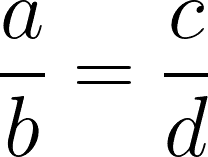
com a, b, c, d ∈ R*, temos que:
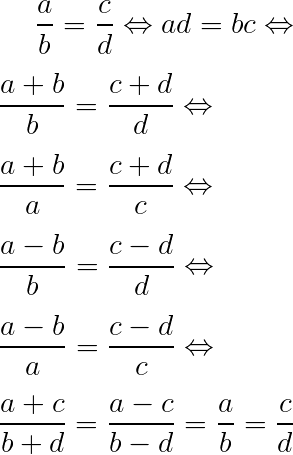
Exemplo:
As razões

e

são equivalentes, logo determinam uma proporção. Então: 12 x 3 = 18 x 2.
Exemplo:
Determine o valor de x na proporção:
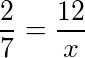
Para resolver esse exemplo e encontrar o valor de x na proporção, vamos utilizar regra de três simples. Assim, pela relação fundamental, temos:

Portanto, x = 42.
Entenda mais sobre proporção, respondendo estes exercícios clicando aqui.
Exercícios resolvidos sobre razão e proporção
(UFOP-MG–2008) Duas torneiras são utilizadas para encher um tanque vazio. Sabendo que sozinhas elas levam 10 horas e 15 horas, respectivamente, para enchê-lo. Quanto tempo às duas torneiras juntas levam para encher o tanque?
- A) 6 horas;
- B) 12 horas e 30 minutos;
- C) 25 horas;
- D) 8 horas e 15 minutos.
Resolução:
A primeira torneira possui uma velocidade de enchimento igual a v1 =
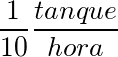
e a segunda torneira, igual a v2 =
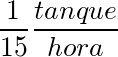
Às duas torneiras juntas encherão o tanque com uma velocidade v1,2 = v1 + v2 =
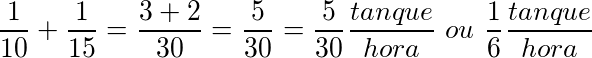
ou seja, encherão 5 tanques em 30 horas, ou 1 tanque em 6 horas.
Alternativa A.
(Unicamp-SP) A quantia de R$ 1.280,00 deverá ser dividida entre 3 pessoas. Quanto receberá cada uma, se
- A) a divisão for feita em partes diretamente proporcionais a 8, 5 e 7?
- B) a divisão for feita em partes inversamente proporcionais a 5, 2 e 10?
Resolução:
Sendo x, y e z a quantia, em reais, que cada pessoa receberá, então:
A)
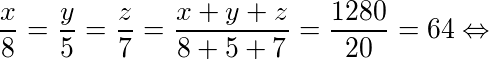
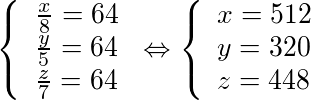
B)
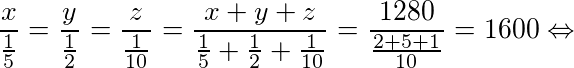
Na matemática um número inverso pode ser representado como a-1 ou 1/a. Por exemplo, o número 5, seu inverso é 5-1 ou 1⁄5.
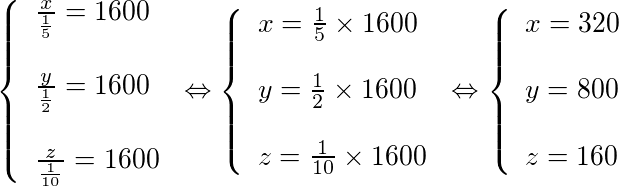
Responda os exercícios propostos para fixar o aprendizado.

